Tìm n: 16^6×2^4=4^2n
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Vì (n+3) ⋮ (n+3) nên để (n+8) ⋮ (n+3) thì: [(n+8) - (n+3)] ⋮ (n+3) hay 5 ⋮ (n+3), Suy ra: n+3 ∈ {1;5}
Vì n + 3 ≥ 3 nên n + 3 = 5 => n = 2
Vậy n = 2
b, Vì 3(n+4) ⋮ (n+4) nên để (16 - 3n) ⋮ (n+4) thì: [(16 - 3n)+3(n+4)] ⋮ (n+4) hay 28 ⋮ (n+4)
Suy ra: n+4 ∈ {1;2;4;7;14;28}
Vì 0 ≤ n ≤6 nên 4 ≤ n+4 ≤ 10.
Từ đó ta có: n+4 ∈ {4;7} hay n ∈ {0;3}
c, Vì 5(9 - 2n) ⋮ (9 - 2n) nên nếu (5n+2) ⋮ (9 - 2n) thì 2(5n+2) ⋮ (9 - 2n)
Suy ra: [5(9 - 2n)+2(5n+2)] ⋮ (9 - 2n) hay 49 ⋮ (9 - 2n) => 9 - 2n ∈ {1;7;49}
Vì 9 - 2n ≤ 9 nên 9 - 2n ∈ {1;7}
Từ đó ta có n ∈ {4;1} với n < 5
Thử lại ta thấy n = 4 hoặc n = 1 đều thõa mãn.
Vậy n ∈ {4;1}

a, Ta có 3(n + 4 ) \(⋮\) (n+ 4)
\(\Rightarrow\) 3(n + 4) = 3n + 12.
Xét tổng (16 - 3n) + (3n + 12)
= 16 - 3n + 3n + 12
= 28 (khử n)
Để (16 - 3n) \(⋮\)(n+4) thì 28 \(⋮\)(n+4)
\(\Rightarrow\) n+ 4\(\in\) Ư(28) = { 1 ; 2 ; 4 ; 7 ; 14 ; 28}
Vì n+ 4 \(\ge\) 4 \(\Rightarrow\) n+4 \(\in\) { 4 ; 7 ; 14 ; 28}
+ n + 4 = 4
n = 4 - 4
n = 0
+ n + 4 = 7
n = 7 - 4
n = 3
+ n + 4 = 14
n = 14 - 4
n = 10
+ n + 4 = 28
n = 28 - 4
n = 24
Vậy n \(\in\) { 0 ; 3 ; 10 ; 24}
b, Làm dạng giống phần a. Hãy động não một chút.

a) 16 - 3n chia hết cho n +4
n+ 4 chia hết cho n+4
=) (16 - 3n ) - ( n + 4) chia hết cho n + 4
16 - 3n - n- 4 chia hết n + 4
12 +4n chia hết cho n +4
= ) n +4 thuộc Ư ( 12 + 4n )
?????
hic mới biết làm tới đây thông cảm

2n=16=>2n=24=>n=4
\(4^{2n+1}=64\Rightarrow4^{2n+1}=4^3\)
\(\Rightarrow2n+1=4\Rightarrow n=\frac{3}{2}\)
c)\(6^n=6\Rightarrow n=1\)
k cho mk nha

a) \(\lim \frac{{ - 2n + 1}}{n} = \lim \frac{{n\left( { - 2 + \frac{1}{n}} \right)}}{n} = \lim \left( { - 2 + \frac{1}{n}} \right) = - 2\)
b) \(\lim \frac{{\sqrt {16{n^2} - 2} }}{n} = \lim \frac{{\sqrt {{n^2}\left( {16 - \frac{2}{{{n^2}}}} \right)} }}{n} = \lim \frac{{n\sqrt {16 - \frac{2}{{{n^2}}}} }}{n} = \lim \sqrt {16 - \frac{2}{{{n^2}}}} = 4\)
c) \(\lim \frac{4}{{2n + 1}} = \lim \frac{4}{{n\left( {2 + \frac{1}{n}} \right)}} = \lim \left( {\frac{4}{n}.\frac{1}{{2 + \frac{1}{n}}}} \right) = \lim \frac{4}{n}.\lim \frac{1}{{2 + \frac{1}{n}}} = 0\)
d) \(\lim \frac{{{n^2} - 2n + 3}}{{2{n^2}}} = \lim \frac{{{n^2}\left( {1 - \frac{2}{n} + \frac{3}{{{n^2}}}} \right)}}{{2{n^2}}} = \lim \frac{{1 - \frac{2}{n} + \frac{3}{{{n^2}}}}}{2} = \frac{1}{2}\)

a) \(4^n=2^{n+1}\)
\(\Rightarrow2^{2n}=2^{n+1}\)
\(\Rightarrow2n=n+1\)
\(\Rightarrow n=1\)
b) \(16=\left(n-1\right)^4\)
\(\Rightarrow2^4=\left(n-1\right)^4\)
\(\Rightarrow n-1=2\)
\(\Rightarrow n=3\)
c) \(125=\left(2n+1\right)^3\)
\(\Rightarrow5^3=\left(2n+1\right)^3\)
\(\Rightarrow2n+1=5\)
\(\Rightarrow2n=4\)
\(\Rightarrow n=2\)
a, 4n = 2n+1
(22)n = 2n+1
22n = 2n+1
2n = n + 1
2n - n = 1
n = 1
b, 16 = (n-1)4
24 = (n-1)4
2 = n-1
n = 3
c, 125 = (2n + 1)3
53 = (2n+1)3
5 = 2n + 1
2n = 4
n = 2

2n+1/n+1 có gt nguyên
<=>2n+2-1/n+1
2(n+1)-1/n+1
2-(1/n+1)
để 2n+1/n+1 có gt nguyên
<=>1/n+1 có gt nguyên
=>n+1 thuộc {+_1}
lm tiếp nhé
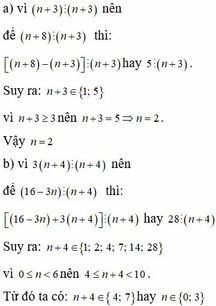

16^6.2^4=4^2n
(2^4)^6.2^4=(2^2)^2n
2^24.2^4=2^4n
2^28=2^4n
=>28=4n
7=n
Vậy n=7
dấu "." là dấu \(\times\)