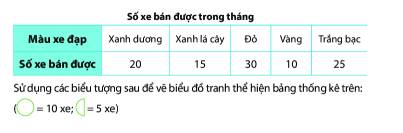
Một cửa hàng bán xe đạp ghi lại số xe bán được trong tháng bằng bảng số liệu sau:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Năm 2019:
+) Số trung bình: \(\overline x = \frac{{54 + 22 + 24 + 30 + 35 + 40 + 31 + 29 + 29 + 37 + 40 + 31}}{{12}} = 33,5\)
+) Phương sai \({S^2} = \frac{1}{{12}}\left( {{{54}^2} + {{22}^2} + ... + {{31}^2}} \right) - 33,{5^2} = 67,25\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 8,2\)
+) Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 22, 24, 29, 29, 30, 31, 31, 35, 37, 40, 40, 54
\({Q_2} = {M_e} = \frac{1}{2}(31 + 31) = 31\)
\({Q_1}\) là trung vị của nửa số liệu: 22, 24, 29, 29, 30, 31. Do đó \({Q_1} = 29\)
\({Q_3}\) là trung vị của nửa số liệu: 31, 35, 37, 40, 40, 54. Do đó \({Q_3} = 38,5\)
\( \Rightarrow {\Delta _Q} = 38,5 - 29 = 9,5\)
Năm 2020:
+) Số trung bình: \(\overline x = 34,5\)
+) Phương sai \({S^2} = \frac{1}{{12}}\left( {{{45}^2} + {{28}^2} + ... + {{37}^2}} \right) - 34,{5^2} = 15,75\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 3,97\)
+) Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 28, 31, 32, 33, 33, 34, 34, 35, 35, 37, 37, 45.
\({Q_2} = {M_e} = \frac{1}{2}(34 + 34) = 34\)
\({Q_1}\) là trung vị của nửa số liệu: 28, 31, 32, 33, 33, 34. Do đó \({Q_1} = 32,5\)
\({Q_3}\) là trung vị của nửa số liệu: 34, 35, 35, 37, 37, 45. Do đó \({Q_3} = 36\)
\( \Rightarrow {\Delta _Q} = 36 - 32,5 = 3,5\)
b) Nhận xét:
So sánh số trung bình: số lượng bán ra trung bình theo tháng không tăng nhiều so với năm trước (tăng 1)
So sánh độ lệch chuẩn: Số lượng xe bán ra năm 2020 không có sự chênh lệch quá nhiều giữa các tháng.
=> Tác động của chiến lược: Số lượng xe bán ra tăng ít, nhưng đồng đều giữa các tháng.
10 tháng 12 2023
a: Sau buổi sáng thì số xe còn lại chiếm:
\(1-\dfrac{3}{7}=\dfrac{4}{7}\)(tổng số xe)
Sau buổi chiều thì số xe còn lại chiếm:
\(\dfrac{4}{7}\cdot\dfrac{3}{4}=\dfrac{3}{7}\)(tổng số xe)
Tổng số xe là: \(12:\dfrac{3}{7}=12\cdot\dfrac{7}{3}=28\left(xe\right)\)
b: Số xe đạp buổi sáng bán được là:
\(28\cdot\dfrac{3}{7}=12\left(xe\right)\)
Số xe đạp buổi chiều bán được là:
28-12-12=4(xe)
KL
22 tháng 11 2019
Số xe đạp để bầy mẫu bằng 1/4 số xe đạp trong kho. Sau khi bán đi 5 chiếc xe đạp để bày mẫu thì số xe đạp để bày mẫu bằng 1/6 số xe trong kho. Vậy 5 chiếc xe đạp đã bán bằng: 1/4 - 1/6 = 1/12 số xe trong kho .
Số xe đạp trong kho là : 5 : 1/12 = 60 chiếc xe đạp.
Số xe để bầy mẫu là : 60 x 1/4 = 15 chiếc xe đạp .
Cửa hàng nhập về : 60 + 15 = 75 chiếc xe đạp .
Đáp số : 75 chiếc xe đạp
Chúc bạn học tốt nhé !
19 tháng 7 2023
40 chiếc xe đạp ứng với phân số là:
\(1-\dfrac{3}{5}-\left(1-\dfrac{1}{3}\right)\times\dfrac{2}{7}=\dfrac{2}{7}\)(số xe đạp)
Tống số xe đạp là:
\(40:\dfrac{2}{7}=140\)(chiếc xe)
đ/s:..
10 tháng 5 2022
Tháng giêng bán được 14 chiếc xe máy.
Số xe máy bán được trong tháng 2 là:
14:2=7 ( chiếc )
Đ/s: 7 chiếc
1 tháng 8 2020
Đáp án:
Giải thích các bước giải:
Ta có:
Số xe đạp làm mẫu bằng 1515 số xe đạp lúc đầu
⇒⇒ Số xe đạp làm mẫu bằng 1414 số xe đạp trong kho
Phân số chỉ số 5 xe đạp so với số xe đạp trong kho là:
14−1614-16 == 112112
Số xe đạp ở trong kho là:
5.125.12 == 6060 (chiếc)
Phân số chỉ số xe đạp trong kho so với số xe đạp nhập về là:
1−151-15 == 4545
Số xe đạp lúc đầu của xe đạp là:
60:4560:45 == 7575 (chiếc)
ĐápĐáp số:số: 7575 chiếc
CHÚC BẠN HỌC TỐT
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Số xe máy cửa hàng đã bán trong tháng tám là:
\(321:\frac{3}{2} =321.\frac{2}{3}= 214\)(chiếc)
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
Tỉ lệ phần trăm số xe đạp sơn màu xanh dương bán được nhiều nhất (chiếm tỉ lệ 60% nhiều nhất), do đó chủ cửa hàng nên đặt hàng thêm cho xe đạp màu xanh dương.
Tham khảo:
Từ bảng thống kê, ta vẽ được biểu đồ tranh như sau: