Với điều kiện nào của m thì các hàm số sau là hàm số bậc nhất
a) f(x)= m2x - m + \(\sqrt{2}\) - x
b) g(x)= m2x + \(\sqrt{3}\) - mx+ m3+ x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Ta có: \(y=\sqrt{m-3}\cdot x+\dfrac{2}{3}\left(m\ge3\right)\)
Để đây là hàm số bậc nhất thì: \(\sqrt{m-3}\ne0\Leftrightarrow m=3\)
Do: \(\sqrt{m-3}\ge0\forall m\ge3\)
Nên với \(m\ge3\) thì y đồng biến trên R
b) Ta có: \(y=\dfrac{\sqrt{m}+\sqrt{5}}{\sqrt{m}-\sqrt{5}}\cdot x+2010\left(m\ge0;m\ne5\right)\)
Để đây là hàm số bậc nhất thì: \(\sqrt{m}-\sqrt{5}\ne0\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\m\ne5\end{matrix}\right.\)
Do \(\sqrt{m}+\sqrt{5}>0\Rightarrow\sqrt{m}-\sqrt{5}< 0\Leftrightarrow m< 5\)
Vậy với 0 ≤ m < 5 thì y nghịch biến trên R

Hàm là bậc nhất khi:
a. \(3m-2\ne0\Rightarrow m\ne\dfrac{2}{3}\)
b. \(3-m>0\Rightarrow m< 3\)
c. \(\left\{{}\begin{matrix}2m-1\ne0\\m+2\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\m\ne-2\end{matrix}\right.\)
d. \(\left\{{}\begin{matrix}m^2-4=0\\m+2\ne0\end{matrix}\right.\) \(\Rightarrow m=2\)
a: ĐKXĐ: \(m\ne\dfrac{2}{3}\)
b: ĐKXĐ: \(m< 3\)
c: ĐKXĐ: \(\left[{}\begin{matrix}m\ge\dfrac{1}{2}\\m< -2\end{matrix}\right.\)
d: ĐKXĐ: \(m=2\)

a, \(\left\{{}\begin{matrix}m\ge0\\\sqrt{m}\ne\sqrt{5}\Leftrightarrow m\ne5\end{matrix}\right.\)
b, Để là hàm số đồng biến thì:\(\dfrac{\sqrt{m}+\sqrt{5}}{\sqrt{m}-\sqrt{5}}>0\Rightarrow\sqrt{m}+\sqrt{5}>0\Leftrightarrow m>5\)

Đáp án A
Ta có: y’ = 3 x 2 + 4 m x + m 2
Hàm số đạt cực tiểu tại x = 1
⇒ y’(1) = 0
⇒ m = -3 hoặc m = -1
Với m = -3, ta có:
y’ = 0 ⇔ x = 1 hoặc x = 3
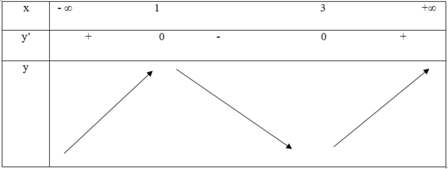
Vậy m = -3 không thoản mãn yêu cầu bài toán
Với m = -1, ta có:
y’ = 0 ⇔ x = 1 hoặc x = 1 3
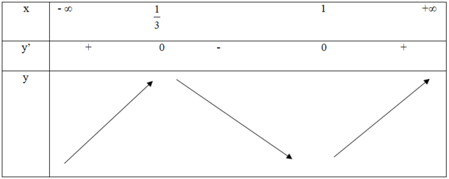
Vậy m = -1 thỏa mãn yêu cầu bài toán

* Ta có :
f(x) = \(m^2x-m+\sqrt{2}-x\) = \(\left(m^2-1\right)x+\sqrt{2}-m\)
Hàm số f(x) là hàm số bậc nhất khi và chỉ khi
\(m^2-1\ne0\)
\(\Leftrightarrow m\ne\pm1\)
* Ta có :
g(x)=\(m^2x+\sqrt{3}-mx+m^3+x\)
= \(\left(m^2-m+1\right)x+m^3+\sqrt{3}\)
Hàm số g(x) là hàm số bậc nhất khi và chỉ khi :
\(m^2-m+1\ne0\)
Vì \(m^2-m+1>0\) với \(\forall m\in R\)
Nên \(m^2-m+1\ne0\) với \(\forall m\in R\)
Vậy Hàm số g(x) là hàm số bậc nhất với \(\forall m\in R\)