a) Quan sát cách tính của Hiếu và Thảo khi rút gọn phân số \(\dfrac{12}{18}\) rồi nêu nhận xét:
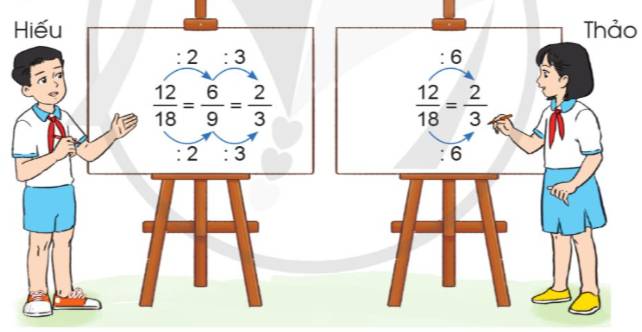
b) Rút gọn phân số \(\dfrac{30}{60}\) về dạng phân số tối giản sử dụng cách làm của Hiếu hoặc của Thảo.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Mẫu số chung nhỏ nhất là 24
b. \(\dfrac{5}{7}\)
c. \(\dfrac{3}{4}\)
d. \(\dfrac{9}{12}\) và giữ nguyên phân số còn lại
e. \(\dfrac{3}{6};\dfrac{4}{6};\dfrac{5}{6}\)
g. \(\dfrac{9}{12};\dfrac{4}{12};\dfrac{2}{12}\)
h. \(\dfrac{15}{60};\dfrac{20}{60};\dfrac{12}{60}\)
i. \(\dfrac{10}{1}\)

a: Các phân số tối giản là \(\dfrac{1}{3};\dfrac{4}{7};\dfrac{72}{73}\) vì ƯCLN(1;3)=1; ƯCLN(4;7)=1; ƯCLN(72;73)=1
b:
Các phân số rút gọn được là
\(\dfrac{8}{12}=\dfrac{8:4}{12:4}=\dfrac{2}{3}\)
\(\dfrac{30}{36}=\dfrac{30:6}{36:6}=\dfrac{5}{6}\)

\(\dfrac{60}{72}=\dfrac{60:12}{72:12}=\dfrac{5}{6}\\ \dfrac{70}{95}=\dfrac{70:5}{95:5}=\dfrac{14}{19}\\ \dfrac{150}{360}=\dfrac{150:30}{360:30}=\dfrac{5}{12}\)

tìm ƯCLN (28;36);(63;90)
Ta có
28=22.7
36=22.32
=> ƯCLN (28:36)=22=4
\(\Rightarrow\frac{28}{36}=\frac{28:4}{36:4}=\frac{7}{9}\)
Ta có:
63=33.7
90=2.32.5
=> ƯCLN (63;90)=32
\(\Rightarrow\frac{-63}{90}=\frac{-63:9}{90:9}=\frac{-7}{10}\)

\(\dfrac{48}{60}=\dfrac{12.4}{12.5}=\dfrac{4}{5}\)
\(\dfrac{-18}{24}=\dfrac{18}{-24}=\dfrac{6.3}{6.\left(-4\right)}=\dfrac{3}{-4}\)
\(\dfrac{25}{-35}=\dfrac{5.5}{5.\left(-7\right)}=\dfrac{5}{-7}\)

a) \(\dfrac{1}{4},\dfrac{6}{5},\dfrac{16}{9}\)
b)
\(\dfrac{4}{10}=\dfrac{2}{5}\)
\(\dfrac{10}{20}=\dfrac{1}{2}\)
\(\dfrac{8}{18}=\dfrac{4}{9}\)
a) Cách rút gọn của Thảo nhanh hơn còn của Hiếu thì lâu hơn vì phải làm nhiều bước
b) Sử dụng cách của Hiếu:
\(\dfrac{30}{60}=\dfrac{30:10}{60:10}=\dfrac{3}{6}=\dfrac{3:3}{6:3}=\dfrac{1}{2}\)
Sử dụng cách của Thảo:
\(\dfrac{30}{60}=\dfrac{30:30}{60:30}=\dfrac{1}{2}\)