TÌm số đo x Biết x H B E K A 55 độ ...
Đọc tiếp
TÌm số đo x Biết
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
28 tháng 10 2023
Lời giải:
a. $x$ là số tự nhiên lớn nhất, $x<18,805$ km nên $x=18$ km
b. $x$ là số tự nhiên lớn nhất, $x< 18,805$ km$ tức là $x< 18805$ m nên $x=18804$ m
BA
2
DX
9 tháng 3 2023
Vì EF//AC :
\(\Rightarrow\dfrac{BF}{BC}=\dfrac{EF}{AC}\Leftrightarrow\dfrac{2}{6}=\dfrac{3}{x}\)
\(\Leftrightarrow2x=3.6=18\)
\(\Rightarrow x=9\left(cm\right)\)
HN
24 tháng 12 2018
\(a,14-5+x=30\)
\(\Rightarrow9+x=30\Rightarrow x=30-9\)
\(\Rightarrow x=21\)
\(b,45-\left(3+x\right)=14\)
\(\Rightarrow3+x=45-14\)
\(\Rightarrow3+x=31\Rightarrow x=31-3\)
\(\Rightarrow x=28\)
\(c,18+\left(-3+x\right)-\left(44-x\right)=55\)
\(\Rightarrow18-3+x-44+x=55\)
\(\Rightarrow2x-29=55\Rightarrow2x=55+29\)
\(\Rightarrow2x=84\Rightarrow x=84:2\)
\(\Rightarrow x=42\)
\(d,\left(x-45\right).27=0\)
\(\Rightarrow x-45=0\Rightarrow x=45\)
P
1
2 tháng 12 2021
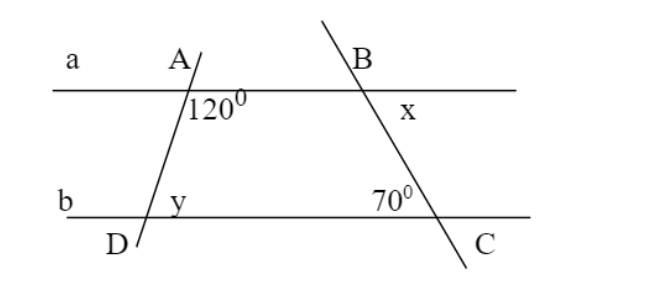
vì a//b nên A+y=180(trong cùng phía
=>y=180-A=180-120=60
vì a//b nên x=C=70(so le trong)
24 tháng 5 2021
Ta thấy ^EHK = ^EHM + ^KHM = ^BAE + ^CAM = ^BAC = 900
Đường thẳng HE: đi qua \(H\left(2;2\right)\), VTPT \(\overrightarrow{HK}\left(1;-1\right)\Rightarrow\) \(HE:x-y=0\)
Xét hệ \(\hept{\begin{cases}x-y=0\\x+y-6=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=3\\y=3\end{cases}}}\Rightarrow E\left(3;3\right)\)
Đường thẳng KE: đi qua \(K\left(3;1\right)\), VTCP \(\overrightarrow{KE}\left(0;2\right)\Rightarrow KE:\hept{\begin{cases}x=3\\y=1+2t\end{cases}}\)
Xét hệ \(\hept{\begin{cases}2x-y-2=0\\x=3\\y=1+2t\end{cases}}\Leftrightarrow\hept{\begin{cases}x=3\\y=4\end{cases}}\Rightarrow A\left(3;4\right)\)
Đường thẳng BC: đi qua \(H\left(2;2\right)\), VTPT \(\overrightarrow{HA}\left(1;2\right)\Rightarrow BC:x+2y-6=0\)(1)
Đường thẳng EB: đi qua \(E\left(3;3\right)\), VTPT \(\overrightarrow{KE}\left(0;2\right)\Rightarrow BE:y=3\)(2)
Đường thẳng KC: đi qua \(K\left(3;1\right)\), VTPT \(\overrightarrow{KE}\left(0;2\right)\Rightarrow KC:y=1\) (3)
Từ (1);(2) suy ra \(B\left(0;3\right)\), từ (1);(3) suy ra \(C\left(4;1\right)\)
Vậy \(A\left(3;4\right),B\left(0;3\right),C\left(4;1\right).\)
M
29 tháng 12 2022
\(\Delta AHE\left(\widehat{AHE}=90^o\right):\widehat{HAE}+\widehat{HEA}=90^o\) (2 góc phụ nhau)
\(\Rightarrow\widehat{HEA}=90^o-55^o=35^o=\widehat{KEB}\)
\(\Delta KBE\left(\widehat{BKE}=90^o\right):\widehat{KBE}+\widehat{KEB}=90^o\) (2 góc phụ nhau)
\(\Rightarrow\widehat{KBE}=90^o-35^o=55^o\)
\(\widehat{KBH}+\widehat{KBE}=180^o\) (2 góc kề bù)
\(\Rightarrow\widehat{KBH}=180^o-55^o=125^o\)