Cho góc xOy = 120°. Lấy điểm A trên tia Ox. Trên cùng nửa mặt phẳng chứa tia Oy bờ là tia Ox, vẽ tia At sao cho góc OAt = 60°. Gọi At' là tia đối của tia At. a) Chứng minh tt' // Oy. b) Gọi Om và An theo thứ tự là các tia phân giác của các góc xOy và xAt. Chứng minh Om // An
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) O A t ^ + x O y ^ = 60°+ 120° = 180° (hai góc trong cùng phía bù nhau)
=> At // Oy => tt' // Oy
b) Vì Om là phân giác x O y ^ nên:
x O m ^ = 1 2 x O y ^ = 1 2 .120° = 60° (1)
Mặt khác : O A t ^ = 60 ° = > x A t ^ = 120°
Vì An là phân giác x A t ^ nên:
x A n ^ = 1 2 x A t ^ = 1 2 .120° = 60° (2)
Từ (1) và (2) suy ra x O m ^ = x A n ^ .
Do đó Om // An
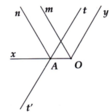

a, Vì \(\widehat{xOy}+\widehat{OAt}=180^0\) mà 2 góc này ở vị trí trong cùng phía nên Oy//At
Mà tt' trùng At nên Oy//tt'
b, Vì Om là p/g xOy nên \(\widehat{xOm}=\dfrac{1}{2}\widehat{xOy}\)
Vì An là p/g tAx nên \(\widehat{xAn}=\dfrac{1}{2}\widehat{tAx}=\dfrac{1}{2}\widehat{xOy}\left(đồng.vị\right)\)
Do đó \(\widehat{xOm}=\widehat{xAn}\) mà 2 góc này ở vị trí đồng vị nên Om//An

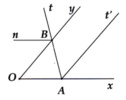
\(a)O\widehat{A}T=80^o\Rightarrow x\widehat{At}=100^{^{ }o}\)
\(\Rightarrow x\widehat{At}'=50^o\)
Do đó,\(x\widehat{O}y=x\widehat{At}'\Rightarrow OY//AT\)
B)\(x\widehat{Oy}=O\widehat{Bn}=50^o\Rightarrow OX//BN\)
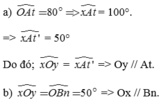

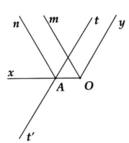
a: \(\widehat{tAO}+\widehat{xOy}=180^0\)
mà hai góc này trong cùng phía
nên tt'//Oy
b: \(\widehat{xAt}+\widehat{tAO}=180^0\)
=>\(\widehat{xAt}=180^0-60^0=120^0\)
=>\(\widehat{xAn}=\dfrac{120^0}{2}=60^0\)
Om là phân giác của góc xOy
=>\(\widehat{xOm}=\dfrac{1}{2}\cdot120^0=60^0\)
\(\widehat{xOm}=\widehat{xAn}\)
mà hai góc này ở vị trí đồng vị
nên Om//An