Câu 1: Người Ai Cập cổ đại đã dùng một lục giác đều nội tiếp trong một hình vuông. Họ tính diện tích hình lục giác này và coi như giá trị xấp xỉ của diện tích hình tròn có đường kính bằng cạnh của hình vuông. Biết 4 cạnh của hình vuông này tiếp xúc với đường tròn và các cạnh lục giác chia hình vuông thành 3 phần bằng nhau. Hãy tính diện tích hình tròn bàn kính r theo cách này ( không dùng số\(\pi\) ). Tính kết quả khi n = 2 để so sánh với công thức dùng số \(\pi\). Theo cách tính trên, em có thể nói rằng số \(\pi\)họ dùng bằng bao nhiêu?
Câu 2: Một quả cầu rơi từ đọ cao 100m. Cứ mỗi lần chạm nền, nó nảy lên \(\frac{3}{5}\)quãng đường. Hỏi quả cầu đi được bao nhiêu mét sau lần thứ năm chạm nền ( trước khi nảy lên ở ô thứ sáu) ?
Câu 3: Một người đàn ông bơi thuyền thể thao, bơi với tốc độ 5km/h ngược dòng sông, với tốc độ nước chảy không đổi. Bỗng nhiên chiếc phao cứu sinh rơi khỏi thuyền, 20 phút sau người đàn ông phát hiện ra điều này và anh vội bơi lui lại lấy, cũng với tốc độ 5km/h. Khi vớt được chiếc phao lên, anh ta thấy rằng chiếc phao ở cách chỗ nó ơi khỏi thuyền là 3km. Hỏi tốc độ dòng nước chảy là bao nhiêu?




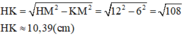
ai trả lời đúng nhanh nhất mk k cho bạn ấy 3 k
xin lỗi bạn mình ko biết làm