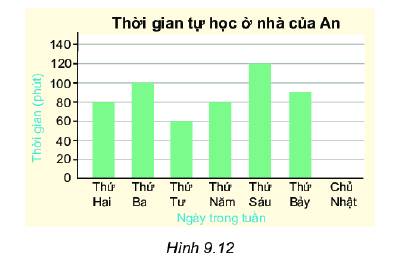
Lập bảng thống kê thể hiện thời gian tự học ở nhà của An vào các ngày trong tuần.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
QT
1
Những câu hỏi liên quan
22 tháng 9 2023
Tham khảo:
a)
b) Không thể tính chính xác, chúng ta chỉ có thể tinh số gần đúng thời gian tự học trung bình của các học sinh trong lớp
c) Giá trị đại diện của nhóm bằng trung bình giá trị đầu mút phải và trái của nhóm đó
Nhóm \( \ge 4.5\) là nhóm mở nên ta dựa theo nhóm gần đó nhất là nhóm [3;4.5) để lấy giá trị đại diện
Số trung binh của mẫu số liệu: : \(\bar x = \frac{{0.75 \times 8 + 2.25 \times 23 + 2.75 \times 6 + 5.25 \times 3}}{{40}} = 2.25\).
CM
1 tháng 9 2019
Thời gian đi từ nhà đến trường của bạn A trong 35 ngày
| Lớp thời gian (phút) | Tần số | Tần suất (%) |
| [19;21) | 5 | 14,29 |
| [21;23) | 9 | 25,71 |
| [23;25) | 10 | 28,57 |
| [25;27) | 7 | 20,00 |
| [27; 29] | 4 | 11,43 |
| Cộng | 35 | 100& |
QT
1
HQ
Hà Quang Minh
Giáo viên
7 tháng 10 2023
Ngày An dành thời gian tự học ở nhà nhiều nhất là thứ sáu vì cột thứ sáu cao nhất và bằng 120 phút.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
Số cuộc gọi của người đó trong một tuần là \(n = 8 + 10 + 7 + 5 + 2 + 1 = 33\).
Gọi \({x_1};{x_2};...;{x_{33}}\) là thời gian thực hiện cuộc gọi của người đó trong một tuần được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_8} \in \left[ {0;60} \right);{x_9},...,{x_{18}} \in \left[ {60;120} \right);{x_{19}},...,{x_{25}} \in \left[ {120;180} \right);{x_{26}},...,{x_{30}} \in \left[ {180;240} \right);\) \({x_{31}},{x_{32}} \in \left[ {240;300} \right);{x_{33}} \in \left[ {300;360} \right)\).
• Tứ phân vị thứ hai của dãy số liệu là: \({x_{17}}\) thuộc nhóm \(\begin{array}{*{20}{l}}{\left[ {60;120} \right)}\end{array}\)
Ta có: \(n = 33;{n_m} = 10;C = 8;{u_m} = 60;{u_{m + 1}} = 120\)
Tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 60 + \frac{{\frac{{33}}{2} - 8}}{{10}}.\left( {120 - 60} \right) = 111\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_8} + {x_9}} \right)\).
Do \({x_8} \in \left[ {0;60} \right),{x_9} \in \left[ {60;120} \right)\) nên tứ phân vị thứ nhất của dãy số liệu là: \({Q_1} = 60\).
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{25}} + {x_{26}}} \right)\).
Do \({x_{25}} \in \left[ {120;180} \right),{x_{26}} \in \left[ {180;240} \right)\) nên tứ phân vị thứ ba của dãy số liệu là: \({Q_3} = 180\).
HQ
Hà Quang Minh
Giáo viên
7 tháng 10 2023
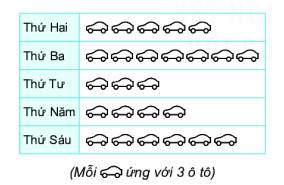
Số ô tô vào gửi ngày
Thứ hai là: 5.3=15 (xe)
Thứ ba là: 7.3=21 (xe)
Thứ tư là: 3.3=9 (xe)
Thứ năm là: 4.3=12 (xe)
Thứ sáu là: 6.3=18 (xe)
Thứ | Hai | Ba | Tư | Năm | Sáu |
Số ô tô | 15 | 21 | 9 | 12 | 18 |
3 tháng 1 2022
Tên cuộc kháng chiến | Thời gian | Lãnh đạo | Chiến thuật | Tướng giặc | Chiến thắng lớn | Kết quả |
Cuộc kháng chiến lần thứ nhất | Năm 1257 đến ngày 29/1/1258 | Trần Thái Tông | Vườn không nhà trống | Ngột Lương Hợp Thai | Đông Bộ Đầu, Quy Hóa | Thắng lợi |
Cuộc kháng chiến lần thứ hai | Năm 1283 đến tháng 5/1285 | Trần Quốc Tuấn | Vườn không nhà trống | Thoát Hoan | Tây Kết, Cửa Hàm Tử, Bến Chương Dương | Thắng lợi |
Cuộc kháng chiến lần thứ ba | Cuối tháng 12/1287 đến tháng 4/1288 | Trần Quốc Tuấn | Vườn không nhà trống, Đóng cọc ở sông Bạch Đằng | Thoát Hoan | Vân Đồn, Bạch Đằng | Thắng lợi |
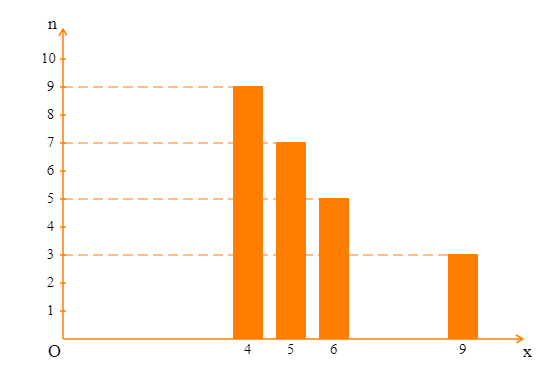
Thời gian An tự học thứ 2 là 80 phút thì ta ghi 80 vào ô ở bên dưới ô ghi “Thứ 2”
Làm tương tự với thời gian An tự học thứ 3, 4, 5, 6, 7 và chủ nhật.
Ngày trong tuần
Thứ 2
Thứ 3
Thứ 4
Thứ 5
Thứ 6
Thứ 7
Chủ Nhật
Thời gian (phút)
80
100
60
80
120
90
0