Cho hàm số y=2/3 x2 có đồ thị P và y= x + 5/3 có đồ thị D a. Vẽ P và D trên cùng một hệ trục toạ độ vuông góc b. Xác định toạ độ các giao điểm của P và D c. Gọi A là điểm thuộcP và B là điểm thuộc D sao cho { x A = x B 11 y A = 8 y B xác định toạ độ của A và B
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 5 2021
Xét pt hoành độ gđ của (P) và (d):
\(x^2=-x+2\)
\(\Leftrightarrow x^2+x-2=0\) \(\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
Thay x=-2 vào (P) ta đc: y=4
Thay x=1 vào (P) ta đc: y=1
Vậy hoành độ gđ của (P) và (d) là (-2;4) và (1;1)
KV
18 tháng 11 2023
a)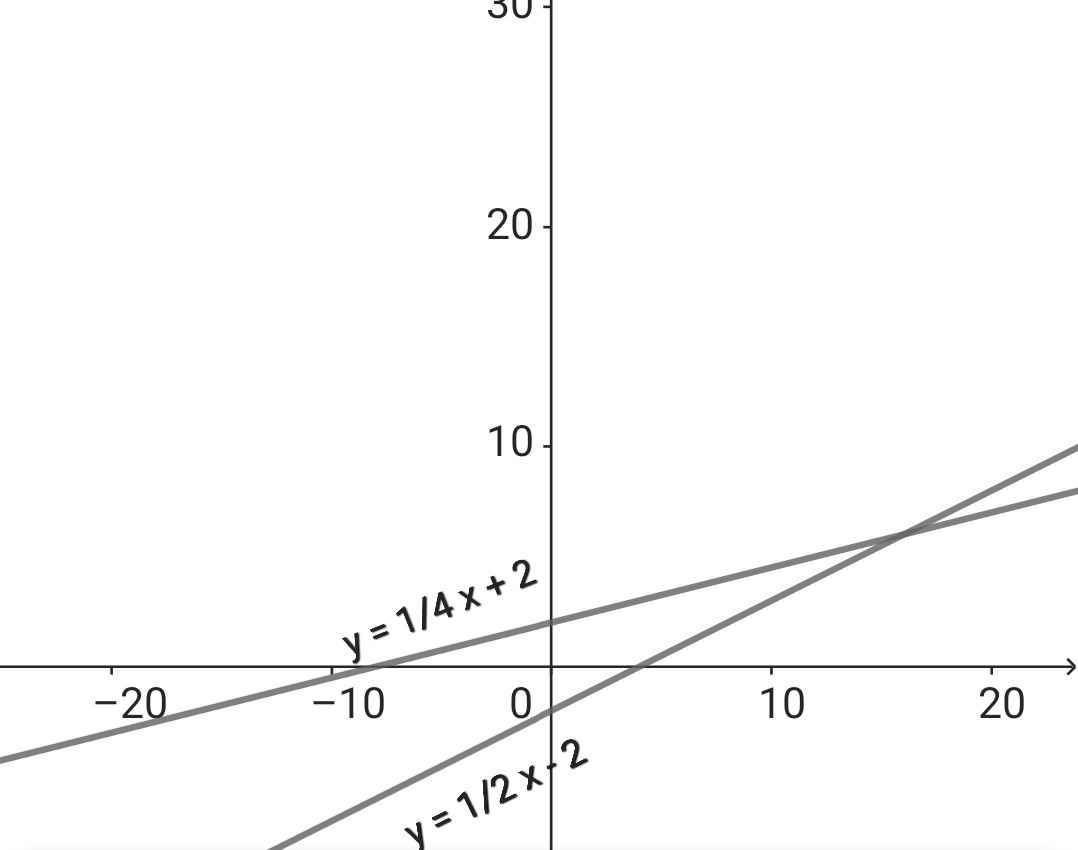 
b) *) Thay x = 0 vào (d) ta có:
y = 1/2 . 0 - 2 = -2
⇒ M(0; -2)
Thay x = 0 vào (d) ta có:
y = 1/4 . 0 + 2 = 2
⇒ N(0; 2)
Phương trình hoành độ giao điểm của (d) và (d)
1/2 x - 2 = 1/4 x + 2
⇔ 1/2 x - 1/4 x = 2 + 2
⇔ 1/4 x = 4
⇔ x = 4 : (1/4)
⇔ x = 16
Thay x = 16 vào (d) ta có:
y = 1/2 . 16 - 2 = 6
⇒ P(16; 6)
31 tháng 3 2021
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=x+2\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow x^2-2x+x-2=0\)
\(\Leftrightarrow x\left(x-2\right)+\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
Thay x=-1 vào (P), ta được:
\(y=\left(-1\right)^2=1\)
Vậy: A(2;4) và B(-1;1)
17 tháng 4 2023
a: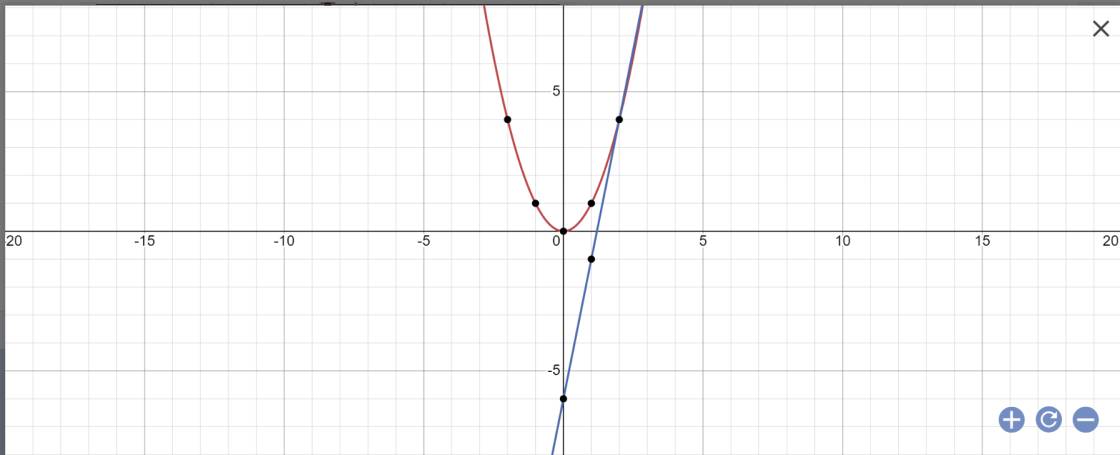 
b: PTHĐGĐ là:
x^2-5x+6=0
=>x=2 hoặc x=3
=>y=4 hoặc y=9
6 tháng 4 2022
b: Phương trình hoành độ giao điểm là:
\(x^2+2x-b=0\)
Δ=4+4b
Để (P) tiếp xúc với (D) thì 4b+4=0
hay b=-1
9 tháng 7 2023
a: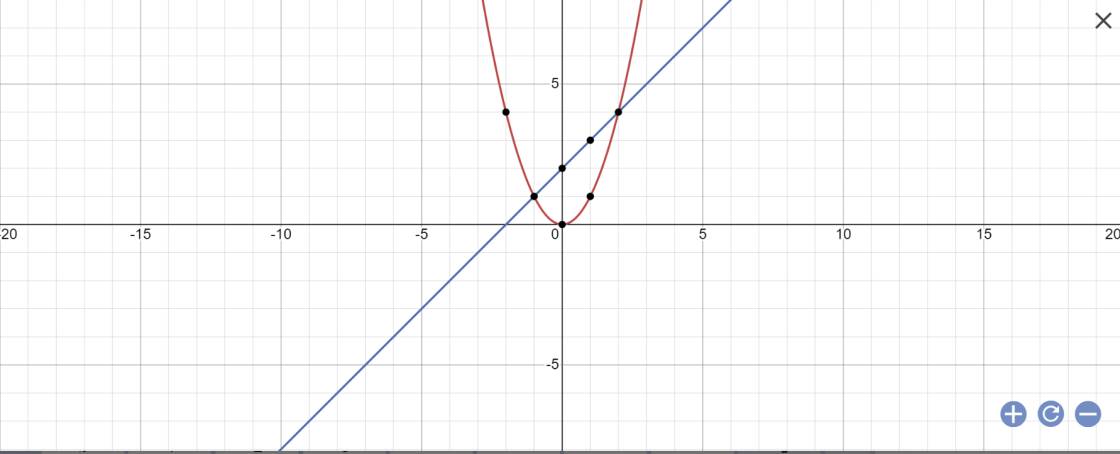 
b: PTHĐGĐ là:
x^2-x-2=0
=>x=2 hoặc x=-1
=>y=4 hoặc y=1