Cho \(\Delta\)ABC nhọn có \(\widehat{A}\) = \(60^0\), M thuộc BC. Kẻ ME \(\bot\) AB, MF \(\bot\) AC, I là trung điểm của AM.a) C/m khi M di chuyển trên cạnh BC thì số đo của góc EIF không đổi.b) Tính độ dài của EF theo AMc) Xác định vị trí của điểm M trên cạnh BC để EF...
Đọc tiếp
Cho \(\Delta\)ABC nhọn có \(\widehat{A}\) = \(60^0\), M thuộc BC. Kẻ ME \(\bot\) AB, MF \(\bot\) AC, I là trung điểm của AM.
a) C/m khi M di chuyển trên cạnh BC thì số đo của góc EIF không đổi.
b) Tính độ dài của EF theo AM
c) Xác định vị trí của điểm M trên cạnh BC để EF min.
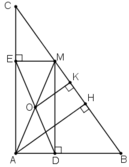
a: góc AEM=góc AFM=90 độ
=>AEMF là tứ giác nội tiếp đường tròn đường kính AM
=>AEMF nội tiếp (I)
Xét (I) có
góc EIF là góc ở tâm chắn cung EF
góc EAF là góc nội tiếp chắn cung EF
Do đó: góc EIF=2*góc EAF=120 độ không đổi
b: Xét ΔEIF có IE=IF
nên ΔIEF cân tại I
=>góc IEF=(180-120)/2=30 độ
Xét ΔIEF có \(\dfrac{IF}{sinIEF}=\dfrac{EF}{sinEIF}\)
=>\(\dfrac{IF}{sin30}=\dfrac{EF}{sin120}\)
=>\(EF=\dfrac{IF}{sin30}\cdot sin120=\dfrac{AM}{2}\cdot\sqrt{3}=AM\cdot\dfrac{\sqrt{3}}{2}\)