Chi tiết vẽ hình nữa ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ΔABC vuông tại A
mà AM là trung tuyến
nên MA=MB=MC=BC/2
Xét ΔMAB có MA=MB và \(\widehat{MBA}=60^0\)
nên ΔMAB đều
b: ΔBAM đều
mà BH là đường cao
nên H là trung điểm của AM
Xét ΔHNM vuông tại H và ΔHBA vuông tại H có
HM=HA
\(\widehat{HMN}=\widehat{HAB}\)(MN//AB)
Do đó: ΔHNM=ΔHBA
=>HN=HB
=>H là trung điểm của BN
Xét tứ giác ABMN có
H là trung điểm chung của AM và BN
BM=BA
Do đó: ABMN là hình thoi
c: ABMN là hình thoi
=>\(\widehat{NMB}=180^0-\widehat{MBA}=180^0-60^0=120^0\)
Xét ΔMNB có \(cosNMB=\dfrac{MN^2+MB^2-BN^2}{2\cdot MN\cdot MB}\)
\(\Leftrightarrow\dfrac{AB^2+AB^2-BN^2}{2\cdot AB\cdot AB}=-\dfrac{1}{2}\)
=>\(2AB^2-BN^2=-AB^2\)
=>\(BN^2=3AB^2\)
Xét ΔMAC có \(cosAMC=\dfrac{MA^2+MC^2-AC^2}{2\cdot MA\cdot MC}\)
=>\(\dfrac{AB^2+AB^2-AC^2}{2\cdot AB\cdot AB}=cos120=\dfrac{-1}{2}\)
=>\(2AB^2-AC^2=-AB^2\)
=>\(AC^2=3AB^2\)
=>\(AC^2=BN^2\)
=>AC=BN

a: Xét ΔBAH và ΔBDH có
BA=BD
AH=DH
BH chung
=>ΔBAD=ΔBDH
b: Xét ΔBAE và ΔBDE có
BA=BD
góc ABE=góc DBE
BE chung
=>ΔBAE=ΔBDE
=>EA=ED và góc BDE=góc BAE=90 độ
=>ΔEAD cân tại E và DE vuông góc BC
c: ED=EA
EA<EM
=>EM>ED
d: Xét ΔBDM vuông tại D và ΔBAC vuông tại A có
BD=BA
góc DBM chung
=>ΔBDM=ΔBAC
=>BM=BC
=>ΔBMC cân tại B
mà BK là trung tuyến
nên BK là phân giác của góc ABC
=>B,E,K thẳng hàng

Bài 1:
a,b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vừa là đường cao, vừa là phân giác
=>góc BAM=góc CAM và AM vuông góc với BC
c: Xét ΔEBC có
EM vừa là đường cao, vừa là trung tuyến
nên ΔEBC cân tại E
d: Xét ΔKCB có
CE là trung tuyến
CE=KB/2
Do đó: ΔKCB vuông tại C
=>KC//AE

Xét hình thang ABCD có EG//AB//CD
nên AE/AD=BG/BC
Xét ΔADC có OE//DC
nên OE/DC=AE/AD
Xét ΔBDC có OG//DC
nên OG/DC=BG/BC
=>OE/DC=OG/DC
=>OE=OG

1:góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
2: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại H
ΔoAC cân tại O
mà OI là trung tuyến
nên OI vuông góc AC
góc BAC=1/2*180=90 độ
góc AHO=góc AIO=góc HAI=90 độ
=>AHOI là hìnhchữ nhật
3:
góc DCA=1/2*sđ cung AC=góc ABC
=>ΔACD đồng dạng vơi ΔCBD
=>CD/BD=AC/BC=2CI/2BO=CI/BO
=>BD/BO=CD/CI

a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của EF
=>E,O,F thẳng hàng
c: Nếu EF cắt BD tại K thì K trùng với O rồi bạn
Xét ΔADC có
AF,DO là trung tuyến
AF cắt DO tại I
Do đó: I là trọng tâm của ΔADC
=>IO=1/3DO
=>\(IK=\dfrac{1}{3}DK\)

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

Chiết suất tuyệt đối của kim cương:
Áp dụng công thức: \(n=\dfrac{c}{v}\)
\(\Rightarrow\)Tôc độ truyền ánh sáng trong kim cương:
\(v=\dfrac{c}{n}=\dfrac{3\cdot10^8}{2,42}=1,24\cdot10^8\)m/s=124000km/h
Chọn B.




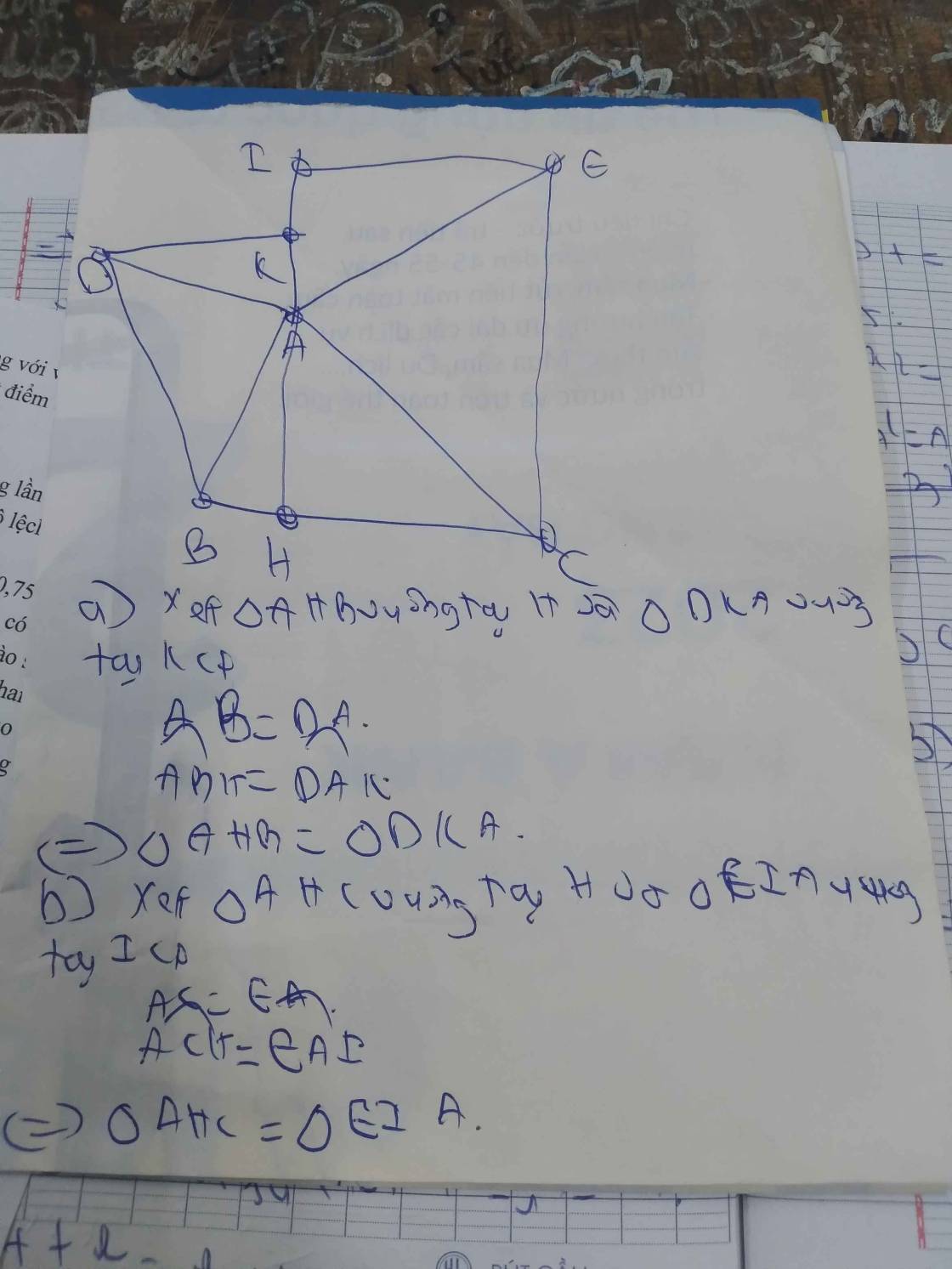



 Vẽ hình và giải chi tiết giúp em với ạ Cảm ơn mọi người nhiều ạ
Vẽ hình và giải chi tiết giúp em với ạ Cảm ơn mọi người nhiều ạ
