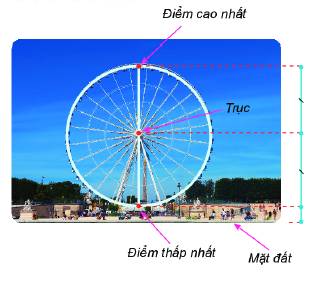
Vòng quay mặt trời trong khu vui chơi Đầm Sen ở thành phố Hồ Chí Minh có điểm cao nhất là 60 m, điểm thấp nhất là 6 m (so với mặt đất). Hỏi trục của vòng quay nằm ở độ cao nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đáy bé là
55:5x3=33(m)
diện tích là
(55+33)x40:2=1760(m2)
số % diện tích vui chơi là
100-40=60%
diện tích vui chơi là
1760:100x60=1056(m2)
đáp số 1056 m2
bài 2
quãng đường quay là:
10x3,14=31,4(m)
đáp số 31,4 m
BÀI 1 : BÀI GIẢI
ĐÁY BÉ CỦA HÌNH THANG LÀ:
\(55\times\frac{3}{5}=33\left(M\right)\)
DIỆN TÍCH HÌNH THANG LÀ :
\(\frac{\left(33+55\right)\times40}{2}=1,76\left(M^2\right)\)
DIỆN TÍCH LÀM NHÀ LÀ :
\(1,76\div100\times40=0,704\left(m^2\right)\)
DIỆN TÍCH LÀM KHU VUI CHƠI LÀ :
\(1,76-0,704=1,056\left(m^2\right)\)
Đ/S : \(1,056\left(m^2\right)\)

Đáp án A
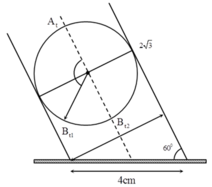
+ Khi A đi từ vị trí cao nhất đến thấp nhất thì mất khoảng thời gian là:
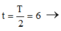 T = 12 s.
T = 12 s.
+ Trong khoảng t = 2 s thì B đi từ Bt1 đến Bt2 như hình vẽ:
![]() B nhanh pha hơn A một góc
B nhanh pha hơn A một góc
+ Từ hình vẽ ta có thể tìm được biên độ dao động của cái bóng là: A = 4 cm.
+ Khi A có vận tốc cực đại (tại vị trí At là VTCB) thì khi đó B đang ở Bt1.
![]()
Và vì B đang đi về VTCB nên v đang tăng

Đáp án A
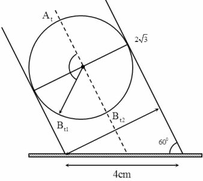
+ Khi A đi từ vị trí cao nhất đến thấp nhất thì mất khoảng thời gian là: t = T/2 = 6s ® T = 12 s.
+ Trong khoảng t = 2 s thì B đi từ B t 1 đến B t 2 như hình vẽ:
® B nhanh pha hơn A một góc ![]()
+ Từ hình vẽ ta có thể tìm được biên độ dao động của cái bóng là: A = 4 cm.
+ Khi A có vận tốc cực đại (tại vị trí A t là VTCB) thì khi đó B đang ở B t 1 .
® ![]()
Và vì B đang đi về VTCB nên v đang tăng.

Gọi hình chiếu của B trên trục là H. Tâm đu quay là O.
Dễ thấy đường kính đu quay là 15 - 3 = 12 (m) nên OB = R = 6m.
Theo định lý Pytago ta có \(OH=\sqrt{OB^2-BH^2}=\sqrt{6^2-2^2}=4\sqrt{2}\) (m).
Gọi hình chiếu của B trên mặt đất là K, N là hình chiếu của O trên mặt đất. Ta có \(BK=HN=HO+ON=4\sqrt{2}+6+3=9+4\sqrt{2}\) (m)
Tương tự ta tính được khoảng cách từ C xuống mặt đất
Vậy....

Đáp án A
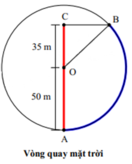
Lúc bắt đầu quay, người đó ở vị trí A, khi đạt độ cao (điểm C) thì người đó đi được quãng đường là L = A B (tô màu xanh)
Tam giác OBC vuông có
cos B O C ⏜ = O C O B = 35 50 ⇒ B O C ⏜ = arccos 7 10
Suy ra A O B ⏜ = π − B O C ⏜ = π − π 180 . a r c c o s 7 10
⇒ L = A B = A O B ⏜ × O A = 50 π 1 − 1 180 . arccos 7 10 m
Mà quay một vòng tròn C = 100 π m hết 15 phút
Do đó, khi đi được Lm sẽ hết L × 15 100 π ≈ 5 , 601 phút

Tham khảo:
Giả sử chiếc đu quay quay theo chiều kim đồng hồ.
Gọi M là vị trí của cabin, M’ là vị trí của cabin sau 20 phút và các điểm A A’, B, H như hình dưới.
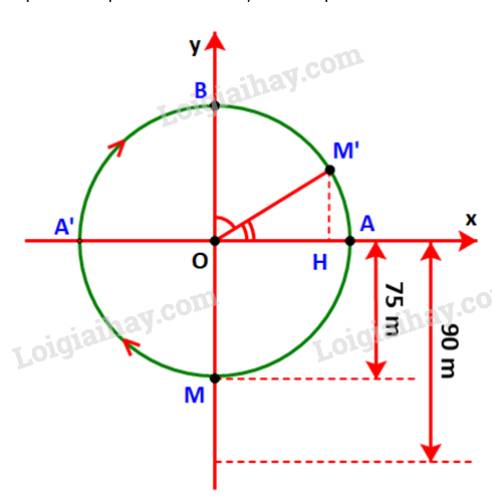
Vì đi cả vòng quay mất 30 phút nên sau 20 phút, cabin sẽ đi quãng đường bằng \(\frac{2}{3}\) chu vi đường tròn.
Sau 15 phút cabin đi chuyển từ điểm M đến điểm B, đi được \(\frac{1}{2}\) chu vi đường tròn.
Trong 5 phút tiếp theo cabin đi chuyển từ điểm B đến điểm M’ tương ứng \(\frac{1}{6}\) chu vi đường tròn hay \(\frac{1}{3}\) cung .
Do đó: \(\widehat {BOM'} = \frac{1}{3}{.180^o} = {60^o}\)\( \Rightarrow \widehat {AOM'} = {90^o} - {60^o} = {30^o}.\)
\( \Rightarrow M'H = \sin {30^o}.OM' = \frac{1}{2}.75 = 37,5\left( m \right).\)
\( \Rightarrow \) Độ cao của người đó là: 37,5 + 90 = 127,5 (m).
Vậy sau 20 phút quay người đó ở độ cao 127,5 m.

sdwadawdddaddddddddawdwadwadadadwadwadwadadadwdwdddddddddaaaaddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddssssssssssssssssssssssssssssssssssssassssssssssssssssssssssssssa
Gọi điểm cao nhất là B, điểm thấp nhất là A, trục là I. Từ hình ta thấy I nằm giữa A và B và IA=IB nên I là trung điểm của AB.
Độ dài đoạn thẳng AB là: 60 - 6 = 54 (m)
Độ dài IA là: 54 : 2 = 27 (m)
Khoảng cách từ mặt đất đến I bằng khoảng cách từ mặt đất đến A + IA.
Trục quay đang nằm ở độ cao : 27 + 6 = 33 (m)