Giải các phương trình và hệ phương trình:

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Thay x = 3, y = 5 vào vế trái của phương trình (3) ta được:
VT = 5.3 – 2.5 = 15 – 10 = 5 = VP
Vậy (x; y) = (3; 5) là nghiệm của phương trình (3).
Hệ phương trình đã cho có nghiệm (x; ) = (3; 5)


Thay x = -3, y = 31/5 vào vế trái của phương trình (2), ta được:
VT = -3.(-3) + 2.31/5 = 9 + 62/5 = 107/5 ≠ 22 = VP
Vậy (x; y) = (-3; 31/5 ) không phải là nghiệm của phương trình (2).
Hệ phương trình đã cho vô nghiệm.

b) x 4 - 5 x 2 + 4 = 0
Đặt t = x 2 ≥ 0 , ta có phương trình:
t 2 - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)
t 1 = 1 (nhận) ; t 2 = 4 (nhận)
với t = 1 ⇔ x 2 = 1 ⇔ x = ± 1
với t = 4 ⇔ x 2 = 4 ⇔ x = ± 2
Vậy nghiệm của phương trình x = ±1; x = ± 2

a) 3 x 2 – 7x + 2 = 0
Δ= 7 2 -4.3.2 = 49 - 24 = 25 > 0 ⇒ ∆ = 5
Phương trình có 2 nghiệm phân biệt:
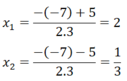
Vậy tập nghiệm của phương trình là S = {2; 1/3}

3:
a: u+v=14 và uv=40
=>u,v là nghiệm của pt là x^2-14x+40=0
=>x=4 hoặc x=10
=>(u,v)=(4;10) hoặc (u,v)=(10;4)
b: u+v=-7 và uv=12
=>u,v là các nghiệm của pt:
x^2+7x+12=0
=>x=-3 hoặc x=-4
=>(u,v)=(-3;-4) hoặc (u,v)=(-4;-3)
c; u+v=-5 và uv=-24
=>u,v là các nghiệm của phương trình:
x^2+5x-24=0
=>x=-8 hoặc x=3
=>(u,v)=(-8;3) hoặc (u,v)=(3;-8)

\(x^2-\left(2-\sqrt{3}\right)x-2\sqrt{3}=0\)
\(\Delta=\left[-\left(2-\sqrt{3}\right)^2\right]-4\left(-2\sqrt{3}\right)\)
\(=\left(4-4\sqrt{3}+3\right)+8\sqrt{3}=7+4\sqrt{3}=\sqrt{3}^2+2.2.\sqrt{3}+2^2=\left(\sqrt{3}+2\right)^2>0\)
=> pt có 2 nghiệm phân biệt
\(\left\{{}\begin{matrix}x_1=\dfrac{2-\sqrt{3}-\sqrt{3}-2}{2}=\dfrac{-2\sqrt{3}}{2}=-\sqrt{3}\\x_2=\dfrac{2-\sqrt{3}+\sqrt{3}+2}{2}=\dfrac{4}{2}=2\end{matrix}\right.\)

Mình mạn phép sửa lại phương trình $2$ của bạn là $mx+3y=1$ nhé.
ĐK: $m\neq 0$
a) Khi $m=2,$ hệ phương trình là:
\(\left\{{}\begin{matrix}-4x+y=5\\2x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+y=5\\4x+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-1\)
b) \(\left\{{}\begin{matrix}-2mx+y=5\\mx+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2mx+y=5\\2mx+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-\dfrac{2}{m}\)
c) Do ta luôn có $y=1$ là số dương nên chỉ cần chọn $m$ sao cho:
\(x=-\dfrac{2}{m}>0\Leftrightarrow m< 0\)
d) \(x^2+y^2=1\Leftrightarrow\left(-\dfrac{2}{m}\right)^2+1^2=1\Leftrightarrow\dfrac{4}{m^2}=0\) (vô lý)
Vậy không tồn tại $m$ sao cho $x^2+y^2=1.$
a)
`x^2+3x+2=0`
`<=>x^2+2x+x+2=0`
`<=>x(x+2)+(x+2)=0`
`<=>(x+2)(x+1)=0`
`<=>x+2=0` hoặc `x+1=0`
`<=>x=-2` hoặc `x=-1`
b)
\(\left\{{}\begin{matrix}x-3y=5\\3x+2y=4\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}3x-9y=15\\3x+2y=4\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}-11y=11\\x-3y=5\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}y=-1\\x-3\cdot\left(-1\right)=5\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}y=-1\\x=2\end{matrix}\right.\)