em cần gấp bài 8 ạ, em cảm ơn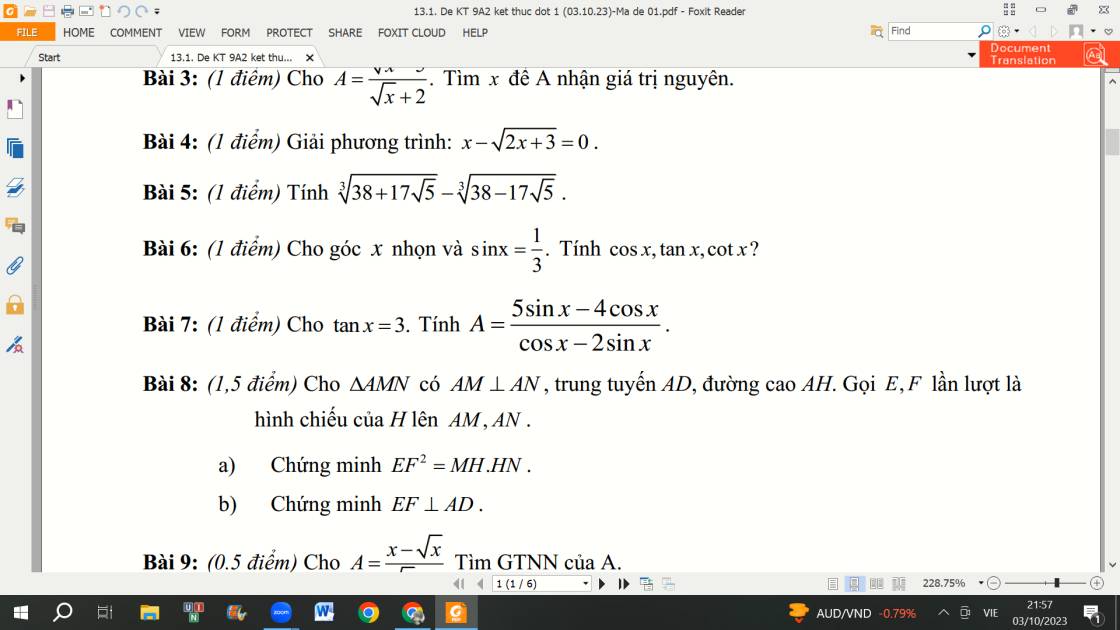
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
V
0
V
0
V
0
KV
3 tháng 10 2023
Bài 6
Ta có:
sin²x + cos²x = 1
⇒ cos²x = 1 - sin²x
= 1 - 1/9
= 8/9
⇒ cosx = 2√2/3
⇒ tanx = sinx : cosx
= 1/3 : 22/3
= √2/4
⇒ cotx = 1 : tanx
= 1 : √2/4
= 2√2
T
3 tháng 10 2023
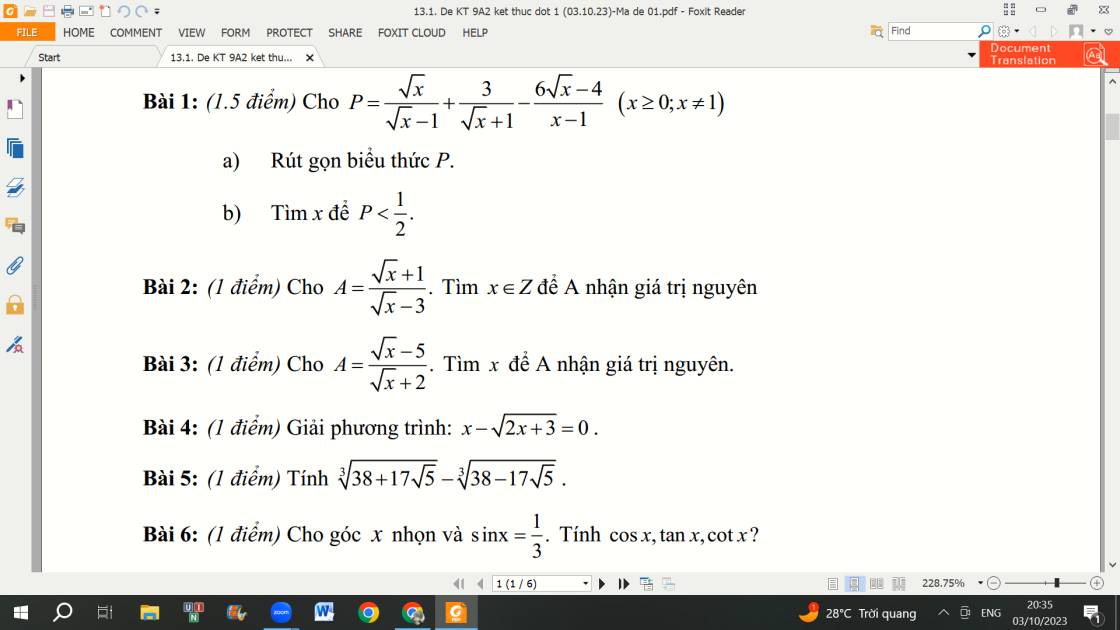
\(a,P=\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}+1}-\dfrac{6\sqrt{x}-4}{x-1}\left(x\ge0;x\ne1\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{6\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x} +1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
\(---\)
\(b,P< \dfrac{1}{2}\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+1}< \dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+1}{2\left(\sqrt{x}+1\right)}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-2-\sqrt{x}-1}{2\left(\sqrt{x}+1\right)}< 0\)
\(\Leftrightarrow\dfrac{\sqrt{x}-3}{2\left(\sqrt{x}+1\right)}< 0\)
\(\Leftrightarrow\sqrt{x}-3< 0\left(vì.2\left(\sqrt{x}+1\right)>0\forall x\ge0\right)\)
\(\Leftrightarrow\sqrt{x}< 3\)
\(\Leftrightarrow x< 9\)
Kết hợp với điều kiện của \(x\), ta được:
\(0\le x< 9;x\ne1\) thì \(P< \dfrac{1}{2}\)
#\(Toru\)
H9
HT.Phong (9A5)
CTVHS
4 tháng 10 2023
Bài 2:
Ta có:
\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{\sqrt{x}-3+4}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\)
A nhận giá trị nguyên khi \(\dfrac{4}{\sqrt{x}-3}\) nguyên:
\(\Rightarrow4\) ⋮ \(\sqrt{x}-3\)
\(\Rightarrow\sqrt{x}-3\inƯ\left(4\right)=\left\{1;-1;2;-2;4;-4\right\}\)
Mà: \(\sqrt{x}-3\ge-3\)
\(\Rightarrow\sqrt{x}-3\in\left\{1;-1;2;-2;4\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{4;2;5;1;7\right\}\)
\(\Rightarrow x\in\left\{16;4;25;1;49\right\}\)
T
3 tháng 10 2023
\(A=\dfrac{\sqrt{x}-5}{\sqrt{x}+2}=\dfrac{\sqrt{x}+2-7}{\sqrt{x}+2}=1-\dfrac{7}{\sqrt{x}+2}\) (ĐK: \(x\ge0\))
Để \(A\) nhận giá trị nguyên thì \(1-\dfrac{7}{\sqrt{x}+2}\) nhận giá trị nguyên
\(\Rightarrow\dfrac{7}{\sqrt{x}+2}\) nhận giá trị nguyên
\(\Rightarrow\sqrt{x}+2\inƯ\left(7\right)\)
\(\Rightarrow\sqrt{x}+2\in\left\{1;7;-1;-7\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{-1;5;-3;-9\right\}\) mà \(\sqrt{x}\ge0\forall x\ge0\)
\(\Rightarrow\sqrt{x}=5\)
\(\Rightarrow x=25\left(tmdk\right)\)
#\(Toru\)
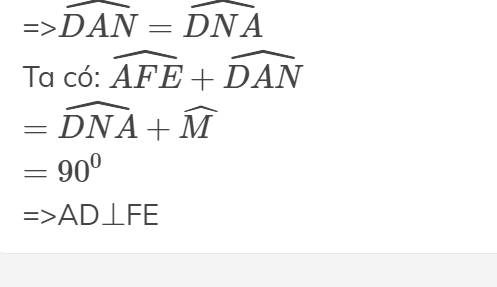
Bài 8:
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>AH=FE
Xét ΔAMN vuông tại A có AH là đường cao
nên \(AH^2=HM\cdot HN\)
=>\(FE^2=HM\cdot HN\)
b: Ta có: AEHF là hình chữ nhật
=>\(\widehat{AFE}=\widehat{AHE}\)
mà \(\widehat{AHE}=\widehat{M}\left(=90^0-\widehat{HAM}\right)\)
nên \(\widehat{AFE}=\widehat{M}\)
Ta có; ΔAMN vuông tại A
mà AD là đường trung tuyến
nên DN=DA
=>\(\widehat{DAN}=\widehat{DNA}\)
Ta có: \(\widehat{AFE}+\widehat{DAN}\)
\(=\widehat{DNA}+\widehat{M}\)
\(=90^0\)
=>AD\(\perp\)FE