giúp em bài 6 với ạ, em cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 10:
a: \(\overrightarrow{AB}+\overrightarrow{BO}+\overrightarrow{OA}\)
\(=\overrightarrow{AO}+\overrightarrow{OA}=\overrightarrow{0}\)
b: \(\overrightarrow{OA}+\overrightarrow{BC}+\overrightarrow{DO}+\overrightarrow{CD}\)
\(=\overrightarrow{OA}+\overrightarrow{DO}+\overrightarrow{BD}\)
\(=\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{BA}\)

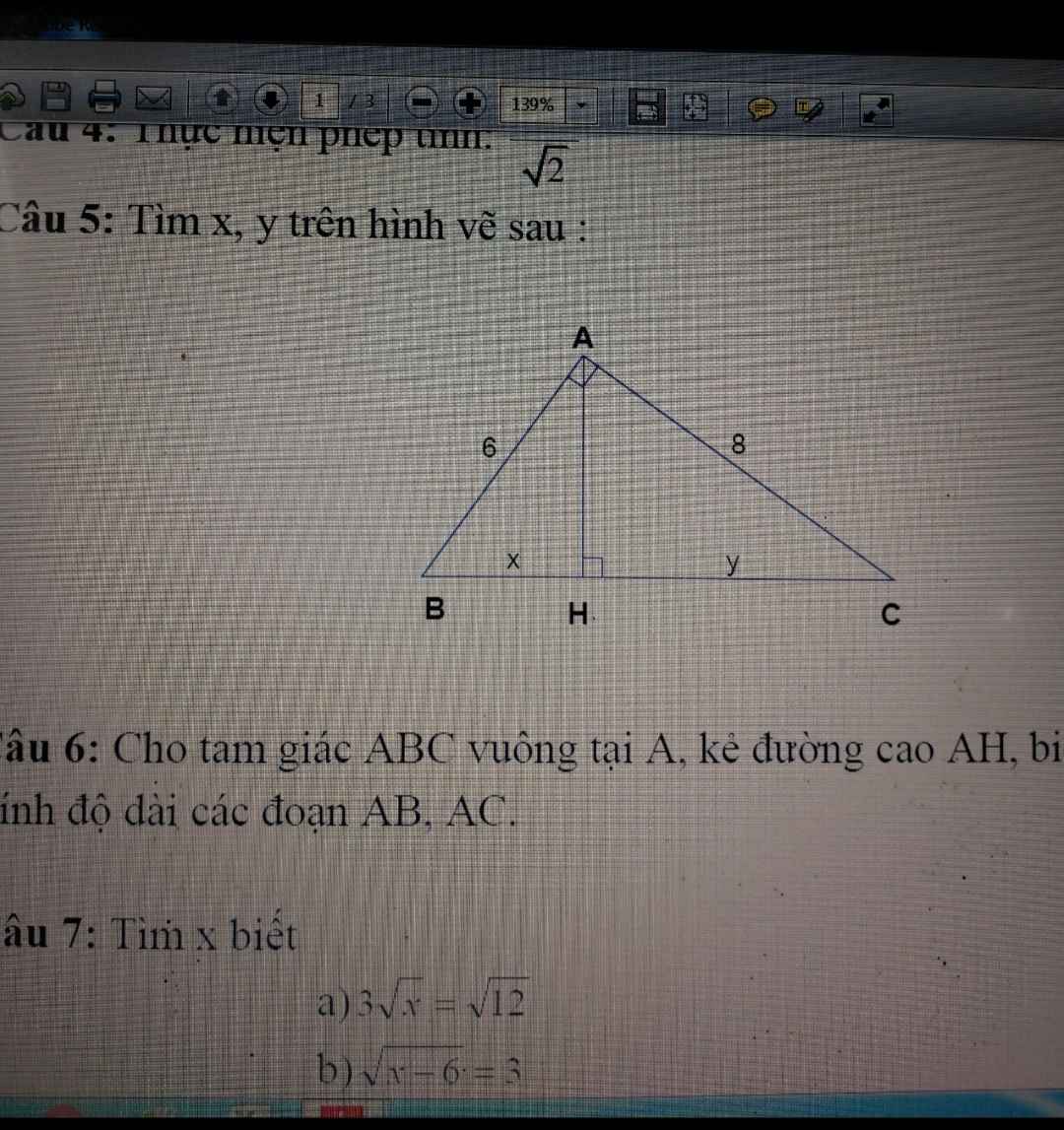
câu 5:
x=3,6
y=6,4
câu 6: chụp lại đề
câu 7:
a)ĐKXĐ: \(x\ge0\)
\(3\sqrt{x}=\sqrt{12}\\ \Rightarrow9x=12\\ \Rightarrow x=\dfrac{4}{3}\)
b) ĐKXĐ: \(x\ge6\)
\(\sqrt{x-6}=3\\ \Rightarrow x-6=9\\ \Rightarrow x=15\)

6:
a: Xét ΔCDM và ΔBAM có
MC=MB
góc CMD=góc BMA
MD=MA
=>ΔCDM=ΔBAM
b: ΔCDM=ΔBAM
=>góc CDM=góc BAM
=>CD//AB
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AC//BD và AC=BD và AB=DC
c: Xét ΔABC có AB>AC
mà HB,HC lần lượt là hình chiếu của AB,AC trên BC
nên HB>HC
Xét ΔECB có HB>HC
mà HB,HC lần lượt là hình chiếu của EB,EC trên BC
nên EB>EC

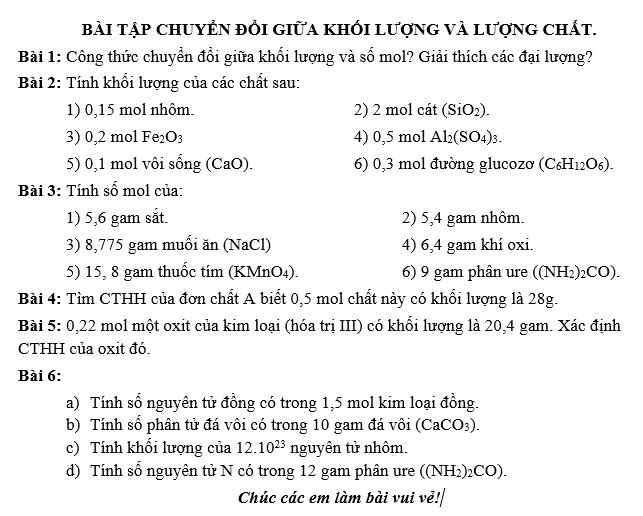
Bài 5:
Gọi kim loại đó là R thì CTHH oxit KL đó là \(R_2O_3\)
\(M_{R_2O_3}=\dfrac{20,4}{0,22}\approx102(g/mol)\\ \Rightarrow M_R=\dfrac{102-3.16}{2}=27(g/mol)\\ \text {Vậy R là nhôm (Al) và CTHH oxit là }Al_2O_3\)
Bài 6:
\(a,1,5.6.10^{-23}=9.10^{-23}(\text {nguyên tử Cu})\\ b,n_{CaCO_3}=\dfrac{10}{100}=0,1(mol)\\ \text {Số phân tử đá vôi là: }0,1.6.10^{-23}=0,6.10^{-23}\\ c,n_{Al}=\dfrac{12.10^{-23}}{6.10^{-23}}=2(mol)\\ \Rightarrow m_{Al}=2.27=54(g)\\ d,\%_N=\dfrac{14.2}{60}.100\%=\dfrac{140}{3}\%\\ \Rightarrow m_{N}=12.\dfrac{140}{3}\%=5,6(g)\\ \Rightarrow n_{N}=\dfrac{5,6}{14}=0,4(mol)\\ \text {Số nguyên tử N là: }0,4.6.10^{-23}=2,4.10^{-23}\)

Bài 13:
góc A=180-80-30=70 độ
=>góc BAD=góc CAD=70/2=35 độ
góc ADC=80+35=115 độ
góc ADB=180-115=65 độ
Bài 14:
Xét ΔABC vuông tại A
-> \(\widehat{B}\)\(+ \widehat{C}=90^o\)
Mà \(\widehat{B}=\widehat{C}\)
=> \(2\widehat{B}=90^o\)
=> \(\widehat{B}=45^o\)

Bài 4:
a. ĐKXĐ: \(\left\{\begin{matrix} x-1\geq 0\\ x-1\neq 2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ x\neq 3\end{matrix}\right.\)
b. \(B=\frac{x-3}{\frac{x-1-2}{\sqrt{x-1}+\sqrt{2}}}=\sqrt{x-1}+\sqrt{2}\)
\(x=4(2-\sqrt{3})\Rightarrow x-1=7-4\sqrt{3}=(2-\sqrt{3})^2\)
\(\Rightarrow \sqrt{x-1}=2-\sqrt{3}\Rightarrow B=\sqrt{x-1}+\sqrt{2}=2-\sqrt{3}+\sqrt{2}\)
c.
$\sqrt{x-1}\geq 0$ với mọi $x\geq 1; x\neq 3$
$\Rightarrow B=\sqrt{x-1}+\sqrt{2}\geq \sqrt{2}$
Vậy $B_{\min}=\sqrt{2}$ khi $x=1$
Bài 5:
\(C=\frac{x-2\sqrt{xy}+y+4\sqrt{xy}}{\sqrt{x}+\sqrt{y}}-\frac{\sqrt{xy}(\sqrt{x}-\sqrt{y})}{\sqrt{xy}}\)
\(=\frac{(\sqrt{x}+\sqrt{y})^2}{\sqrt{x}+\sqrt{y}}-(\sqrt{x}-\sqrt{y})=(\sqrt{x}+\sqrt{y})-(\sqrt{x}-\sqrt{y})\)
\(=2\sqrt{y}\) vẫn phụ thuộc vào biến $y$ bạn ạ. Bạn xem lại đề.

Hệ có nghiệm duy nhất khi \(m^2\ne1\Rightarrow m\ne\pm1\)
Khi đó: \(\left\{{}\begin{matrix}x+my=m+1\\m^2x+my=3m^2-m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+my=m+1\\\left(m^2-1\right)x=3m^2-2m-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{3m+1}{m+1}\\y=\dfrac{m-1}{m+1}\end{matrix}\right.\)
Đặt \(P=xy=\dfrac{\left(3m+1\right)\left(m-1\right)}{\left(m+1\right)^2}=\dfrac{3m^2-2m-1}{\left(m+1\right)^2}=\dfrac{-\left(m+1\right)^2+4m^2}{\left(m+1\right)^2}\)
\(=-1+\left(\dfrac{2m}{m+1}\right)^2\ge-1\)
\(P_{min}=-1\) khi \(m=0\)

a: AD vuông góc CD
SA vuông góc CD
=>CD vuông góc (SAD)
Kẻ AH vuông góc SD
=>CD vuông góc AH
mà SD vuông góc AH
nên AH vuông góc (CDS)
=>d(A;(SCD))=AH=căn (4a^2+16a^2/8a^2)=căn 10/2
Kẻ MP//AB//CD
=>AP/AD=AM/AC
=>AP/4a=1/4
=>AP=a
=>PD=3a
PQ vuông góc SD
PQ vuông góc CD
=>PQ vuông góc (SCD)
mà PM//(SCD)
nên d(P;(SCD))=PQ
Xét ΔADH có PQ/AH=PD/AD
\(\dfrac{PQ}{\sqrt{10}:2}=\dfrac{3a}{4a}=\dfrac{3}{4}\)
=>PQ=3 căn 10/8
=>d(M;(SCD))=PQ=3căn 10/8
Kẻ NG//AM
Kẻ GU vuông góc SD
=>d(G;(SCD))=GU
GU/AH=SG/SA=1/2
=>GU=căn 10/4
b: (SCD;ABCD))=(AD;SD)=góc ADH
AH=AD*cosADH
=>cosADH=căn 10/8
=>góc ADH=67 độ
(SBD;(ABCD))=góc SOA
SA=AO*tan SOA
=>tan SOA=2/5
=>góc SOA=22 độ




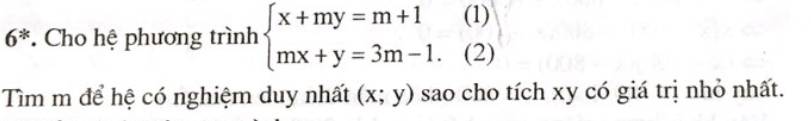
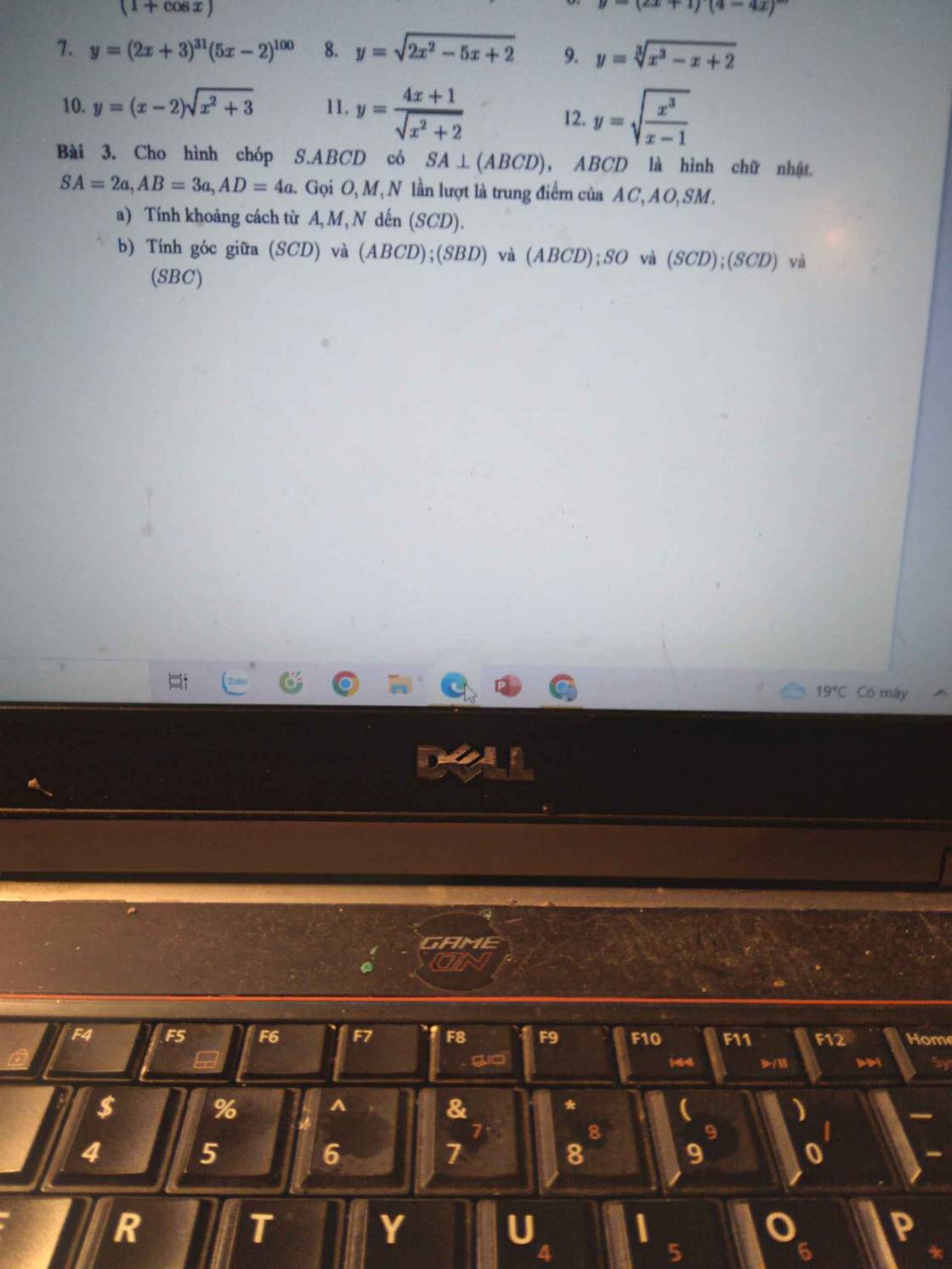 Giúp em bài 3 với ạ. Em cảm ơn ạ
Giúp em bài 3 với ạ. Em cảm ơn ạ
Bài 6:
Ta có:
\(sin^2x+cos^2x=1\)
\(\Leftrightarrow cos^2x=1-sin^2x\)
\(\Leftrightarrow cos^2x=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9}\)
\(\Leftrightarrow cosx=\sqrt{\dfrac{8}{9}}=\dfrac{2\sqrt{2}}{3}\)
Mà: \(tanx=\dfrac{sinx}{cosx}\)
\(\Leftrightarrow tanx=\dfrac{1}{3}:\dfrac{2\sqrt{2}}{3}=\dfrac{1}{2\sqrt{2}}=\dfrac{\sqrt{2}}{4}\)
\(\Leftrightarrow\text{c}otx=\dfrac{1}{tanx}=1:\dfrac{\sqrt{2}}{4}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)