Biết ƯCLN(75, 105) = 15, hãy tìm ƯC(75, 105).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 10 2023
a: \(50=2\cdot5^2;75=5^2\cdot3\)
=>\(ƯCLN\left(50;75\right)=5^2=25\)
=>\(ƯC\left(50;75\right)=Ư\left(25\right)=\left\{1;5;25\right\}\)
\(x\inƯC\left(50;75\right)\)
=>\(x\in\left\{1;5;25\right\}\)
mà x<=20
nên \(x\in\left\{1;5\right\}\)
b: \(35=5\cdot7;105=3\cdot5\cdot7\)
=>\(ƯCLN\left(35;105\right)=5\cdot7=35\)
\(35⋮x;105⋮x\)
=>\(x\inƯC\left(35;105\right)\)
=>\(x\inƯ\left(35\right)\)
=>\(x\in\left\{1;5;7;35\right\}\)
mà x>5
nên \(x\in\left\{7;35\right\}\)
c: \(144=2^4\cdot3^2;192=2^6\cdot3;240=2^4\cdot3\cdot5\)
=>\(ƯCLN\left(144;192;240\right)=2^4\cdot3=48\)
\(144⋮x;192⋮x;240⋮x\)
=>\(x\inƯC\left(144;192;240\right)\)
mà x lớn nhất
nên x=ƯCLN(144;192;240)=48
d: \(54=3^3\cdot2;14=2\cdot7\)
=>\(ƯCLN\left(54;14\right)=2\)
\(x\inƯC\left(54;14\right)\)
mà x lớn nhất
nên x=ƯCLN(54;14)
=>x=2
VN
Võ Ngọc Phương
VIP
12 tháng 11 2023
Ta có:
\(40=2^3.5\)
\(75=3.5^2\)
\(105=3.5.7\)
\(ƯCLN\left(40;75;105\right)=5\)
\(BCNN\left(40;75;105\right)=2^3.3.5^2.7=8.3.25.7=4200\)
M
24 tháng 8 2023
Để giải thích tại sao Cx // Bt và Az // By, chúng ta cần xem xét các góc đã cho và quan sát các quy tắc và định lý liên quan đến góc và đường thẳng trong hình học.
a) Cx // Bt: Theo giả thiết, C1^ = 75 độ và A4^ = 105 độ. Ta biết rằng trong một tam giác, tổng các góc trong một tam giác bằng 180 độ. Vì vậy, B1^ = 180^ - C1^ = 180^ - 75^ = 105^.
Theo quy tắc, nếu hai góc cùng nằm bên trái hoặc cùng nằm bên phải của một đường chéo và chúng có cùng độ lớn, thì các cặp đường thẳng song song với nhau. Trong trường hợp này, C1^ và B1^ đều nằm bên trái của đường chéo và có cùng độ lớn 105 độ. Vì vậy, chúng ta có Cx // Bt.
b) Az // By: Theo giả thiết, C1^ = 75 độ và 132^ = 105 độ. Tương tự như trên, ta có B2^ = 180^ - 132^ = 48^.
Chúng ta cũng biết rằng hai góc đối nhau của một hình chữ Z có cùng độ lớn. Trong trường hợp này, A4^ và B2^ là hai góc đối nhau của hình chữ Z và cùng có độ lớn 105 độ. Vì vậy, chúng ta có Az // By.
Tóm lại, chúng ta có Cx // Bt do C1^ = B1^ và Az // By do A4^ = B2^.
BN
1
CT
2
QD
25 tháng 12 2016
a) 220 = 22 . 5 . 11
240 = 24 . 3 . 5
300 = 22 . 3 . 52
=> ƯCLN(220;240;300) = 22 . 5 . 3 = 60
=> BCNN(220;240;300) = 24 . 5 . 11 . 3 = 2640
b) 40 = 23 . 5
75 = 3 . 52
105 = 3 . 5 .7
=> ƯCLN(40;75;105) = 5 . 3 = 15
=> BCNN(40;75;105) = 23 . 52 . 3 . 7 = 4200
c) 18 = 2 . 32
36 = 22 . 32
72 = 23 . 32
=> ƯCLN(18;36;72) = 2 . 32 = 18
=> BCNN(18;36;72) = 23 . 32 = 72
PP
2
T
7 tháng 2 2021
a) Ta có: 18=2⋅3^21
24=2^3⋅3
30=2⋅3⋅5
Do đó: ƯCLN(18;24;30)=2⋅3=6 và BCNN(18;24;30)=2^3⋅3^2⋅5=360
b) Ta có: 40=2^3⋅5
75=3⋅5^2
105=3⋅5⋅7105=3⋅5⋅7
Do đó: ƯCLN(40;75;105)=5^1=5 và BCNN(40;75;105)=2^3⋅3⋅5^2⋅7=4200
c) Ta có: 18=2⋅3^2
36=2^2⋅3^2
72=2^3⋅3^2
Do đó: ƯCLN(18;36;72)=2.3^2=2⋅9=18 và BCNN(18;36;72)=2^3⋅3^2=72
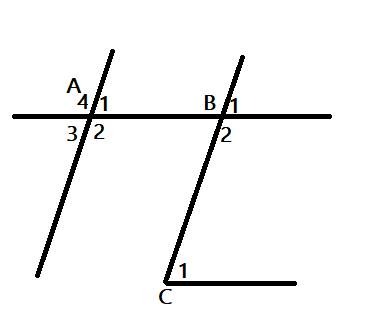
ƯC(75, 105) = Ư(15) = {1; 3; 5; 15}.