Chọn ngẫu nhiên một gia đình có ba con và quan sát giới tính của ba người con này.
Tính xác suất của các biến cố sau:
a) A: “Con đầu là gái";
b) B: “Có ít nhất một người con trai".
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Sơ đồ tư duy:
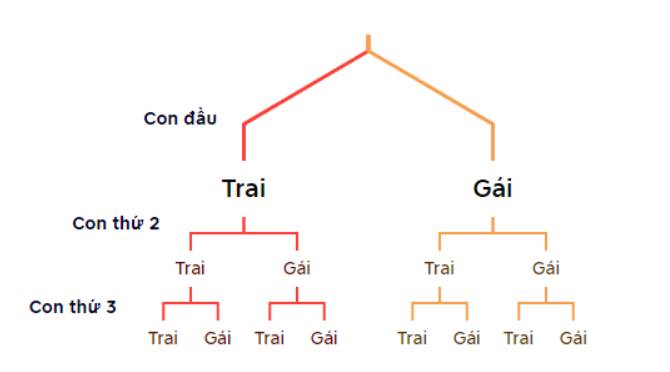
Kí hiệu con trai: T, con gái: G.
Các kết quả có thể xảy ra là: GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT.
Do đó: \(\Omega\)= {GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT}.
Vậy n(Ω) = 8.
b) Gọi biến cố A: “Gia đình đó có một con trai và hai con gái”.
Ta có: A = {GTG; TGG; GGT}. Do đó, \(n(A)\)= 3.
Vậy \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{3}{8}\)

Lời giải:
1. Xác suất để gia đình đó có 3 con trai = xác suất để trong 4 người con còn lại có 1 con trai và 3 con gái và bằng:
$0,5.0,5.0,5.0,5=0,0625$
2. Nhà đó đã có sẵn 2 con trai
Xác suất để nhà đó chỉ có 2 con trai (4 còn lại là nữ): $0,5.0,5.0,5.0,5=0,0625$
Xác xuất để nhà đó có 3 con trai: $0,0625$ (đã cm ở 1)
Xác suất để nhà đó có tối đa 3 con trai: $0,0625.2=0,125$

a: \(\Omega=\left\{1;2;3;...;20\right\}\)
\(A=\left\{2;3;5;7;11;13;17;19\right\}\)
=>n(A)=8
=>P(A)=8/20=2/5
b: B={1;4;9;16}
=>n(B)=4
=>P(B)=4/20=1/5

Trong 5 ngày đầu tháng 9/2021 dựa vào biểu đồ ta thấy có duy nhất ngày 3/9 có lượng điện tiêu thụ là 10kWh . Nên chọn ngẫu nhiên 1 ngày lượng tiêu thụ điện 10kWh thì xác suất chọn được là \(\dfrac{1}{5}\)

a/Những chấm là số chẵn: \(2;4;6\)
\(\rightarrow\)Có 3 mặt là số chẵn
Xác suất của biến cố A:
\(3:6=\dfrac{1}{2}\)
b/Chấm vừa chia hết cho 2 vừa chia hết cho 3: \(6\)
\(\rightarrow\)Có 1 mặt là số vừa chia hết cho 2 vừa chia hết cho 3
Xác suất của biến cố B:
\(1:6=\dfrac{1}{6}\)
c/Chấm không phải là số nguyên tố và là ước của 24: \(4\) ; \(6\)
\(\rightarrow\)Có 2 mặt không phải là số nguyên tố và là ước của 24
Xác suất của biến cố C:
\(2:6=\dfrac{1}{3}\)
Ta có: \(\Omega = \left\{ {TGT;TTG;TTT;TGG;GGT;GTG;GTT;GGG} \right\}\) nên suy ra \(n\left( \Omega \right) = 8\).
a) Ta có \(A = \left\{ {GGT;GTG;GTT;GGG} \right\}\). Suy ra \(n\left( A \right) = 4\).
Từ đó, \(P\left( A \right) = \frac{4}{8} = \frac{1}{2}\).
b) Gọi biến cố \(B\): “Có ít nhất một con trai”.
Ta có \(B = \left\{ {TGT;TTG;TTT;TGG;GGT;GTG;GTT} \right\}\). Suy ra \(n\left( B \right) = 7\).
Từ đó, \(P\left( B \right) = \frac{7}{8}\).