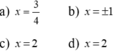Cho P=(x/x2-36 - x-6/x2+6x): 2x-6/x2+6x + x/6-x a) rút gọn P b)tìm x để P= -1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KH
9 tháng 6 2021
a)
\(S=\left(\dfrac{x}{x^2-36}-\dfrac{x-6}{x^2+6x}\right):\dfrac{2x-6}{x^2+6x}+\dfrac{x}{6-x}\)
\(S=\left(\dfrac{x}{\left(x+6\right)\left(x-6\right)}-\dfrac{x-6}{x\left(x+6\right)}\right)\cdot\dfrac{x\left(x+6\right)}{2\left(x-3\right)}-\dfrac{x}{x-6}\)
\(S=\left(\dfrac{x^2-\left(x-6\right)^2}{x\left(x+6\right)\left(x-6\right)}\right)\cdot\dfrac{x\left(x+6\right)}{2\left(x-3\right)}-\dfrac{x}{x-6}\)
\(S=\left(\dfrac{x^2-x^2+12x-36}{x\left(x+6\right)\left(x-6\right)}\right)\cdot\dfrac{x\left(x+6\right)}{2\left(x-3\right)}-\dfrac{x}{x-6}\)
\(S=\dfrac{12\left(x-3\right)}{x\left(x+6\right)\left(x-6\right)}\cdot\dfrac{x\left(x+6\right)}{2\left(x-3\right)}-\dfrac{x}{x-6}\)
\(S=\dfrac{6}{x-6}-\dfrac{x}{x-6}\)
\(S=\dfrac{6-x}{x-6}=-1\)
b) Vì giá trị của biểu thức S không phụ thuộc vào giá trị của biến nên với mọi giá trị của x ta đều có giá trị của S là - 1.
14 tháng 11 2021
\(a,ĐK:x\ne3;x\ne-2\\ b,A=\dfrac{\left(x-3\right)^2}{\left(x-3\right)\left(x+2\right)}=\dfrac{x-3}{x+2}\\ c,A\in Z\Leftrightarrow\dfrac{x+2-5}{x+2}=1-\dfrac{5}{x+2}\in Z\\ \Leftrightarrow x+2\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow x\in\left\{-7;-3;-1;3\right\}\left(tm\right)\)
KM
1
31 tháng 5 2022
Câu 1:
\(\left(a-b\right)\left(a^2+ab+b^2\right)-\left(a^3+b^3\right)\)
\(=a^3-b^3-a^3-b^3\)
\(=-2b^3\)
Câu 2:
a: \(x^2-6x+9=0\)
\(\Leftrightarrow\left(x-3\right)^2=0\)
=>x-3=0
hay x=3
b: \(x^2-\dfrac{2}{5}x+\dfrac{1}{25}=0\)
\(\Leftrightarrow x^2-2\cdot x\cdot\dfrac{1}{5}+\dfrac{1}{25}=0\)
\(\Leftrightarrow\left(x-\dfrac{1}{5}\right)^2=0\)
=>x-1/5=0
hay x=1/5
HN
18 tháng 12 2019
A = \(\left(\frac{x}{x^2-36}-\frac{x-6}{x^2+6x}\right):\frac{2x-6}{x^2+6x}+\frac{x}{6-x}\)
= \(\left[\frac{x}{\left(x-6\right)\left(x+6\right)}-\frac{x-6}{x\left(x+6\right)}\right]:\frac{2\left(x-3\right)}{x\left(x+6\right)}-\frac{x}{x-6}\)
= \(\left[\frac{x^2}{x\left(x-6\right)\left(x+6\right)}-\frac{\left(x-6\right)^2}{x\left(x-6\right)\left(x+6\right)}\right]:\frac{2\left(x-3\right)}{x\left(x+6\right)}-\frac{x}{x-6}\)
= \(\frac{x^2-\left(x-6\right)^2}{x\left(x-6\right)\left(x+6\right)}:\frac{2\left(x-3\right)}{x\left(x+6\right)}-\frac{x}{x-6}\)
= \(\frac{\left(x-x+6\right)\left(x+x-6\right)}{x\left(x-6\right)\left(x+6\right)}:\frac{2\left(x-3\right)}{x\left(x+6\right)}-\frac{x}{x-6}\)
=
HN
18 tháng 12 2019
= \(\frac{x\left(2x-6\right)}{x\left(x-6\right)\left(x+6\right)}:\frac{2x-6}{x\left(x+6\right)}-\frac{x}{x-6}\)
= \(\frac{2x-6}{\left(x-6\right)\left(x+6\right)}.\frac{x\left(x+6\right)}{2x-6}\) \(-\frac{x}{x-6}\)
= \(\frac{x}{x-6}-\frac{x}{x-6}\)
= 0
PN
15 tháng 5 2021
\(|x-6|=-5x+9\)
Xét \(x\ge6\)thì \(pt< =>x-6=-5x+9\)
\(< =>x-6+5x-9=0\)
\(< =>6x-15=0\)
\(< =>x=\frac{15}{6}\)(ktm)
Xét \(x< 6\)thì \(pt< =>x-6=5x-9\)
\(< =>4x-9+6=0\)
\(< =>4x-3=0< =>x=\frac{3}{4}\)(tm)
Vậy ...