cho đường thẳng (d) y=(2m-n)x+m+n-3 hãy xác định M và n đường thẳng (d) đi qua hai điểm (2;3) và (-1;4)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. Với $m=1$ thì ptđt $(d)$ là: $y=x+1$
b. Trung điểm của 2 đường thẳng??? Đường thẳng thì làm gì có trung điểm hả bạn? Đoạn thẳng thì có.
c. $(d)$ cắt $y=x-2$ tại điểm có hoành độ $-1$
$\Leftrightarrow$ PT hoành độ giao điểm $(2-m)x+2m-1-(x-2)=0$ nhận $x=-1$ là nghiệm
$\Leftrightarrow (2-m)(-1)+2m-1-(-1-2)=0$
$\Leftrightarrow m=0$

b: Phương trình hoành độ giao điểm là:
-x+3=-2x+1
\(\Leftrightarrow x=-2\)
Thay x=-2 vào y=-x+3, ta được;
y=2+3=5
Thay x=-2 và y=5 vào (d), ta được:
\(-2\left(2-m\right)+2m-1=5\)
\(\Leftrightarrow2m-4+2m-1=5\)
\(\Leftrightarrow4m=10\)
hay \(m=\dfrac{5}{2}\)

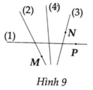
-Đường thẳng a là đường thẳng số 2
-Đường thẳng b là đường thẳng số 1
-Đường thẳng c là đường thẳng số 3
-Đường thẳng d là đường thẳng số 4

Đường thẳng a là đường thăng số (2). Đường thẳng b là đường thẳng số (1). Đường thẳng c là đường thẳng số (3).

Đường thẳng a là đường thăng số (2). Đường thẳng b là đường thẳng số (1). Đường thẳng c là đường thẳng số (3).
Cho đường thẳng( d):y(m+1)x+2m-3 Cm rằng vs mọi gt m đường thẳng d luôn luôn đi qua một điểm cố định

Thay x=2 và y=3 vào (d), ta được:
\(2\left(2m-n\right)+m+n-3=3\)
=>4m-2n+m+n=6
=>5m-n=6(1)
Thay x=-1 và y=4 vào (d), ta được:
\(\left(-1\right)\cdot\left(2m-n\right)+m+n-3=4\)
=>-2m+n+m+n=7
=>-m+2n=7(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}5m-n=6\\-m+2n=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5m-n=6\\-5m+10n=35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9n=41\\5m-n=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}n=\dfrac{41}{9}\\5m=n+6=\dfrac{41}{9}+6=\dfrac{41}{9}+\dfrac{54}{9}=\dfrac{95}{9}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=\dfrac{19}{9}\\n=\dfrac{41}{9}\end{matrix}\right.\)