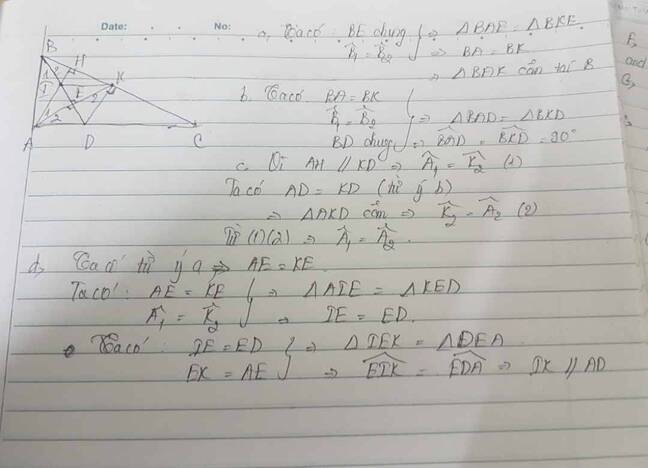Cho tam giác ABC vuông ở A , đường phân giác BD . Kẻ DK vuông góc với BC tại K .
a) Chứng minh tam giác BAD = tam giác BKD
b) Chứng minh tam giác BAK cân
c) Kẻ Ah vuông góc với BC tại H . Chứng minh AK là tia phân giác của góc HAC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
9 tháng 5 2022
a. Xét Δ ABE và Δ KBE có:
^B1=^B2(BD là tia p/g)
^BEA=^KEB=90o
AE chung
=> ΔABE=ΔKBE(g.c.g)
=>AB=KB
=>ΔABK cân tại B
(xin lỗi mình ko biết phần b,c,d) ;-;
cho bạn cái hình nè :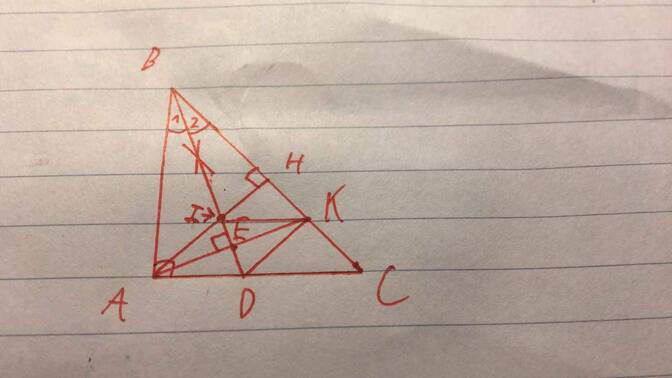
28 tháng 5 2018
Hình Bé tự vẽ nhé :v
a,
Xét tg BAE và tg BEK có:
+) Góc (BEA)= góc (BKE)
+) Góc (EBA)= góc (EBK)
+ BE chung
=> hai tg trên bằng nhau.
=> BA=BK
=> Tg BAK cân tại B
b,
Xét tg (BAD) và tg (BKD) có:
+) BA=BK ( cmt )
+) Góc (ABD)= góc (DBK)
+) BD chung
=> Hai tg này bằng nhau
=> Góc (BAD)= Góc (BKD)
Mà Góc (BAD)=90 độ => BKD =90 độ
=> DK vuông góc với BC
CB
2 tháng 5 2019
chỉ cần giải cho mình câu c,d thôi nha !!!
A - ri - ga - to ^-^
7 tháng 4 2020
Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
LA
8 tháng 4 2020
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A
10 tháng 4 2022
a: Xét ΔBAK có
BE là đường cao
BE là đường trung tuyến
Do đó: ΔBAK cân tại B
b: Xét ΔBAD và ΔBKD có
BA=BK
\(\widehat{ABD}=\widehat{KBD}\)
BD chung
Do đó: ΔBAD=ΔBKD
Suy ra: \(\widehat{BAD}=\widehat{BKD}=90^0\)
T
9 tháng 7 2020
a.Xét hai tam giác vuông ABE và tam giác vuông KBE có
góc ABE = góc KBE = 90độ
cạnh BE chung
góc ABE = góc KBE [ gt ]
Do đó ; tam giác ABE = tam giác KBE [ g.c.g ]
\(\Rightarrow\) AB = KB [ cạnh tương ứng ]
Vậy tam giác ABK cân tại B
b.Xét tam giác ABD và tam giác KBD có
AB = KB [ vì tam giác ABE = tam giác KBE theo câu a ]
góc ABD = góc KBD [ vì BD là tia phân giác góc B ]
cạnh BD chung
Do đó ; tam giác ABD = tam giác KBD [ c.g.c ]
\(\Rightarrow\)góc BAD = góc BKD [ góc tương ứng ]
mà bài cho góc BAD = 90độ nên góc KBD = 90độ
Vậy DK vuông góc với BC
c.Vì DK vuông góc với BC và AH vuông góc với BC nên
DK // AH
Suy ra ; góc HAK = góc DKA [ ở vị trí so le trong ] [ 1 ]
Mặt khác ; AD = DK [ vì tam giác ABD = tam giác KBD ]
\(\Rightarrow\)tam giác ADK là tam giác cân tại D nên
góc DKA = góc DAK [ 2 ]
Từ [ 1 ] và [ 2 ] suy ra
góc HAK = góc DAK
Vậy AK là tia pg góc KAD hay AK là tia pg góc HAC
5 tháng 5 2019
ban tu ve hinh
a) +) tam giac ABE co : ABE+BAE+BEA=180( dinh li tong 3 goc cua 1 tam giac)
ABE+BAE+90=180
ABE+BAE =180-90=90(1)
+) tam giac EBK co : EBK+KEB+BKE=180(dinh li tong 3 goc cua 1 tam giac )
EBK+90+BKE=180
EBK+BKE=90(2)
Vi ABE=EBK(BD la phan giac cua ABC) nen tu (1) va (2) suy ra BAE=BKE
suy ra tam giac BAK can tai B
b)Vi tam giac ABK can tai B nen AB=BK
xet tam giac ABD va tam giac KBD CO :
BD chung
ABD=KBD ( BD la phan giac cua ABC)
AB=AK(cmt)
NEN tam giac ABD= tam giaac KBD (c-g-c) nen AB=BK( 2 canh tuong ung ) ;BAD=BKD(2 goc tuong ung ) ma BAD=90 NEN DKB=90
SUY RA DK vuong goc voi BC
CAC GOC KO CO KI HIEU MU GOC BAN TU THEM VAO