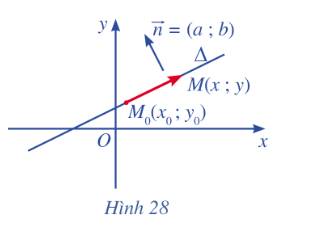
Cho điểm \(M\left( {{x_o};{y_0}} \right)\) và đường thẳng \(\Delta :{\rm{a}}x + by + c = 0\) có vecto pháp tuyến \(\overrightarrow n = \left( {{\rm{a }};{\rm{ b}}} \right)\left( {\overrightarrow n \ne 0} \right)\)
Gọi H là hình chiếu vuông góc của M trên \(\Delta \).
a) Chưng minh rằng \(\left| {\overrightarrow n .\overrightarrow {HM} } \right| = \sqrt {{a^2} + {b^2}} .HM\)
b) Giả sử H có tọa độ \(\left( {{x_1};{y_1}} \right)\). Chứng minh rằng \(\overrightarrow n .\overrightarrow {HM} = a\left( {{x_o} - {x_1}} \right) + b\left( {{y_o} - {y_1}} \right) = a{x_o} + b{y_o} + c\)
c) Chứng minh rằng \(HM = \frac{{\left| {{\rm{a}}{x_o} + b{y_o} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

a) Ta có: \(\left| {\overrightarrow n .\overrightarrow {HM} } \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {HM} } \right|.\left| {\cos \left( {\overrightarrow n ,\overrightarrow {HM} } \right)} \right| = \sqrt {{a^2} + {b^2}} .HM.1 = \sqrt {{a^2} + {b^2}} .HM\)
b) Ta có : \(\overrightarrow n = \left( {{\rm{a }};{\rm{ b}}} \right)\left( {\overrightarrow n \ne 0} \right){\rm{ ,}}\overrightarrow {HM} = \left( {{x_1} - {x_o};{y_1} - {y_o}} \right) \Rightarrow \overrightarrow n .\overrightarrow {HM} = a\left( {{x_o} - {x_1}} \right) + b\left( {{y_o} - {y_1}} \right) = a{x_o} + b{y_o} + c\) trong đó \(a{x_1} + b{y_1} = c\).
c) Ta có: \(\left| {\overrightarrow n .\overrightarrow {HM} } \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {HM} } \right|.\left| {\cos \left( {\overrightarrow n ,\overrightarrow {HM} } \right)} \right| \Leftrightarrow \left| {a{x_o} + b{y_o} + c} \right| = \sqrt {{a^2} + {b^2}} .HM \Rightarrow HM = \frac{{\left| {a{x_o} + b{y_o} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)