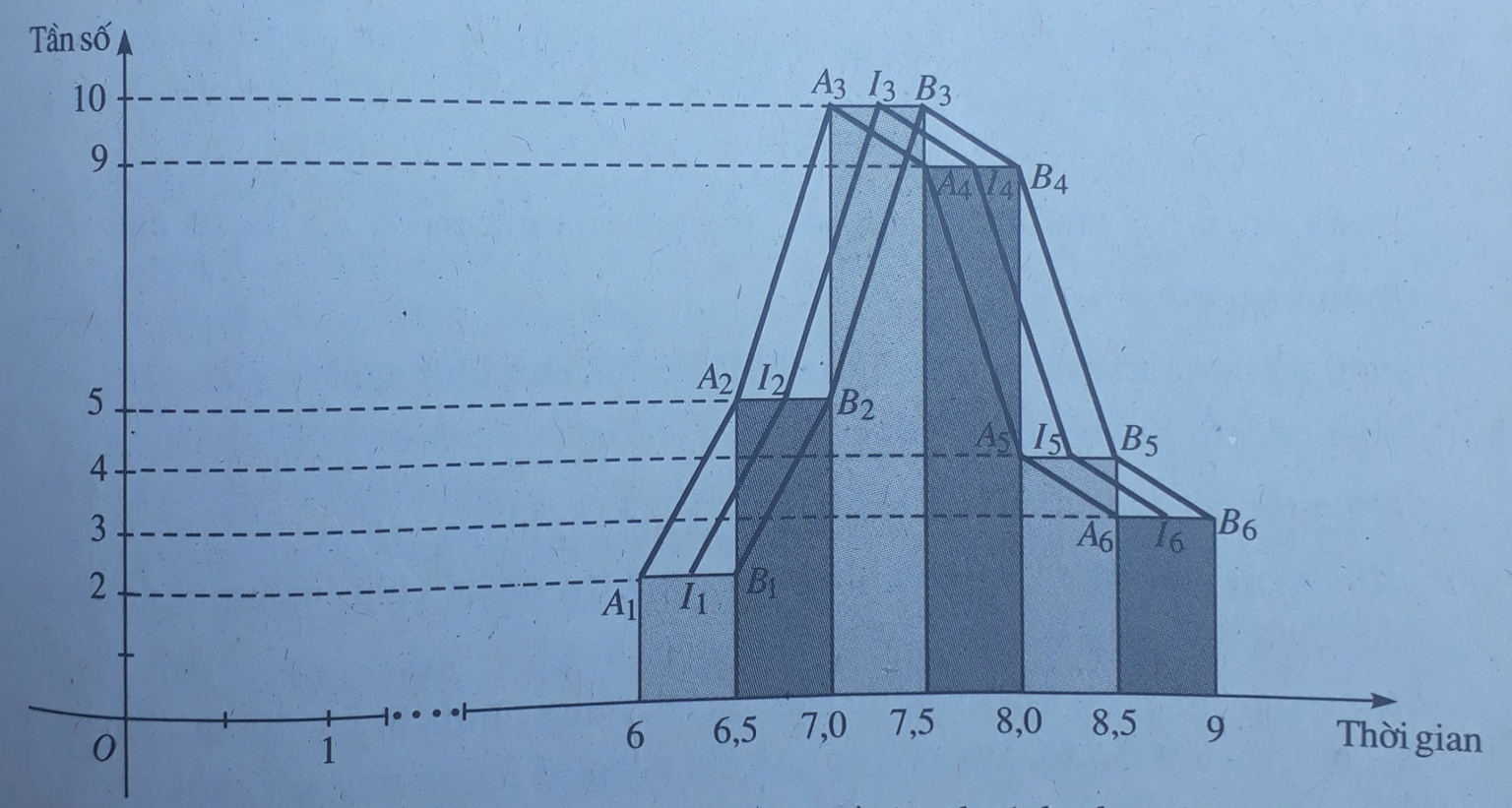
Hãy tính một số số đo thống kê mô tả được liệt kê trong Bnagr T.2 của mẫu số liệu về thời gian sử dụng mạng xã hội:
Giá trị nhỏ nhất | \({Q_1}\) | Số trung bình | Trung vị | \({Q_3}\) | Mốt | Giá trị lớn nhất |
|
|
|
|
|
|
|
Dựa trên những số đặc trưng tính được, hãy nêu nhận xét về thời gian sử dụng mạng xã hội của các học sinh được khảo sát.


Giá trị nhỏ nhất
\({Q_1}\)
Số trung bình
Trung vị
\({Q_3}\)
Mốt
Giá trị lớn nhất
30
60
72
67,5
90
60
120
Cụ thể:
Số trung bình \(\frac{{60 + 30 + ... + 60}}{{30}} = 72\)
Bước 1: Sắp xếp mẫu số thành dãy không giảm ta được: 30, 30, 30, 30, 45, 45, 45, 60, 60, 60, 60, 60, 60, 60, 60, 75, 75, 75, 80, 80, 80, 90, 90, 90, 90, 120, 120, 120, 120, 120.
Bước 2: Cỡ mẫu n = 30
Trung vị \({M_e} = \frac{1}{2}\left( {60 + 75} \right) = 67,5\)
\({Q_1} = {x_8} = 60\)
\({Q_3} = {x_{23}} = 90\)
Nhận xét:
+) Trung bình mỗi bạn sử dụng mạng xã hội khoảng 72 phút/ ngày.
+) Sự chênh lệch thời gian sử dụng giữa các bạn là khá lớn.