Cho điểm (\({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\)) nằm trên đường tròn (C) tâm I(a; b) bán kính R. Gọi \(\Delta \) là tiếp tuyến tại điểm \({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\) thuộc đường tròn (Hình 44).a) Chứng tỏ rằng \(\overrightarrow {I{M_o}} \) là vectơ pháp tuyến của đường thẳng \(\Delta \).b) Tính toạ độ của \(\overrightarrow {I{M_o}} \).c) Lập phương trình tổng quát của đường thẳng \(\Delta...
Đọc tiếp
Cho điểm (\({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\)) nằm trên đường tròn (C) tâm I(a; b) bán kính R. Gọi \(\Delta \) là tiếp tuyến tại điểm \({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\) thuộc đường tròn (Hình 44).
a) Chứng tỏ rằng \(\overrightarrow {I{M_o}} \) là vectơ pháp tuyến của đường thẳng \(\Delta \).
b) Tính toạ độ của \(\overrightarrow {I{M_o}} \).
c) Lập phương trình tổng quát của đường thẳng \(\Delta \).
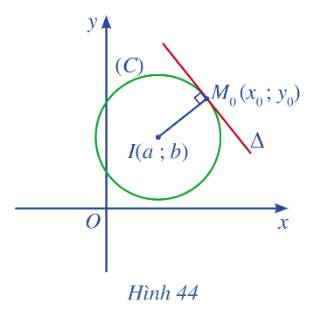
a) Do \(\Delta \) là pháp tuyến của đường tròn (C) tại điểm \({M_o}\) nên \(\Delta \) vuông góc với \(I{M_o}\). Vậy \(\overrightarrow {I{M_o}} \) là vectơ pháp tuyến của đường thẳng \(\Delta \).
b) Tọa độ \(\overrightarrow {I{M_o}} = \left( {{x_o} - a;{y_o} - b} \right)\)
c) Đường thẳng \(\Delta \)đi qua điểm \({M_o}\)và có vecto pháp tuyến \(\overrightarrow {I{M_o}} \)là: \(\left( {{x_o} - a} \right)\left( {x - {x_o}} \right) + \left( {{y_o} - b} \right)\left( {y - {y_o}} \right) = 0\)