Vẽ các elip sau
a) \(\frac{{{x^2}}}{{10}} + \frac{{{y^2}}}{4} = 1\)
b) \(\frac{{{x^2}}}{{12}} + \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình hypebol theo cú pháp x^2/10 - y^2/6 = 1 vào vùng nhập lệnh ta được hình hypebpl dưới đây:

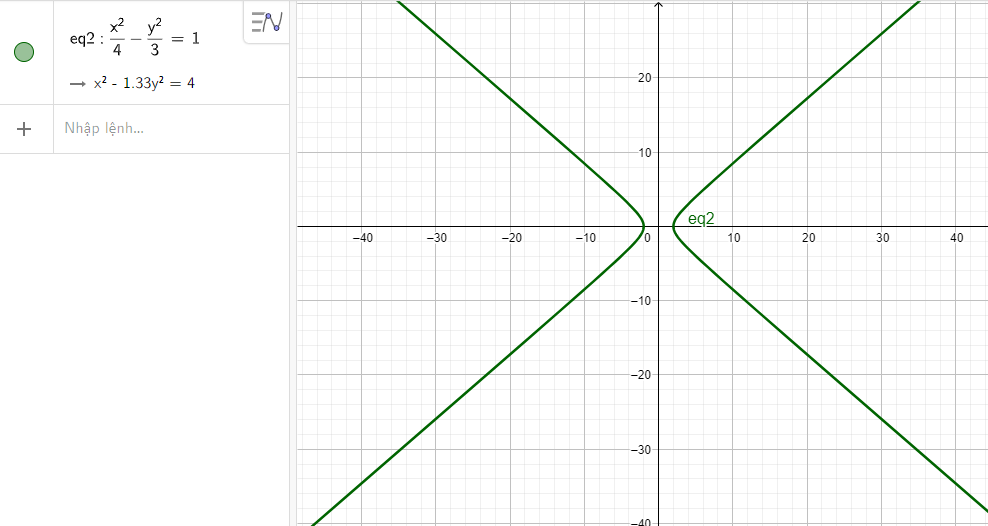
b) Nhập phương trình hypebol theo cú pháp x^2/4 - y^2/3 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:
c) Nhập phương trình hypebol theo cú pháp x^2/64 - y^2/36 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:


a) Phương trình \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\) đã có dạng phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) nên ta có: \(a = 10,b = 6 \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt {{{10}^2} - {6^2}} = 8 \)
Suy ra ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 8;0} \right),{F_2}\left( {8;0} \right)\)
Tọa độ các đỉnh: \(A(0;6),B(10;0),C(0; - 6),D( - 10;0)\)
Độ dài trục lớn 20
Độ dài trục nhỏ 12
b) Phương trình \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\) đã có dạng phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) nên ta có: \(a = 5,b = 4 \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt {{5^2} - {4^2}} = 3\)
Suy ra ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 3;0} \right),{F_2}\left( {3;0} \right)\)
Tọa độ các đỉnh: \(A(0;4),B(5;0),C(0; - 4),D( - 5;0)\)
Độ dài trục lớn 10
Độ dài trục nhỏ 8
c) \({x^2} + 16{y^2} = 16 \Leftrightarrow \frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{1} = 1\)
Vậy ta có phương trình chính tắc của elip đã cho là \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{1} = 1\)
Suy ra \(a = 4,b = 1 \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt {{4^2} - {1^2}} = \sqrt {15} \)
Từ đó ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - \sqrt {15} ;0} \right),{F_2}\left( {\sqrt {15} ;0} \right)\)
Tọa độ các đỉnh: \(A(0;1),B(4;0),C(0; - 1),D( - 4;0)\)
Độ dài trục lớn 8
Độ dài trục nhỏ 2

1
Ez lắm =)
Bài 1:
Với mọi gt \(x,y\in Q\) ta luôn có:
\(x\le\left|x\right|\) và \(-x\le\left|x\right|\)
\(y\le\left|y\right|\) và \(-y\le\left|y\right|\Rightarrow x+y\le\left|x\right|+\left|y\right|\) và \(-x-y\le\left|x\right|+\left|y\right|\)
Hay: \(x+y\ge-\left(\left|x\right|+\left|y\right|\right)\)
Do đó: \(-\left(\left|x\right|+\left|y\right|\right)\le x+y\le\left|x\right|+\left|y\right|\)
Vậy: \(\left|x+y\right|\le\left|x\right|+\left|y\right|\)
Dấu "=" xảy ra khi: \(xy\ge0\)

Phương trình chính tắc của elip là: c) \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{25}} = 1\).
a) Không là PTCT vì a =b =8
b) Không là PTCT
d) Không là PTCT vì a =5 < b =8.

1. \(\frac{-7}{12}\)< \(\frac{x-1}{4}\)< \(\frac{2}{3}\)
=> \(\frac{-7}{12}\)< \(\frac{3.\left(x-1\right)}{12}\)< \(\frac{8}{12}\)
=> 3 . ( x - 1 ) thuộc { - 6 ; - 5 ; - 4 ; - 3 ; - 2 ; - 1 ; 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7}
Lập bảng tính giá trị x , cái này dễ lên bạn tự làm nha
1/ \(-\frac{7}{12}< \frac{x-1}{4}< \frac{2}{3}\)
hay \(\frac{-7}{12}< \frac{3.\left(x-1\right)}{12}< \frac{8}{12}\)
Vậy \(-7< 3.\left(x-1\right)< 8\)
Vậy \(3.\left(x-1\right)\in\left\{-6;-5;-4;...;7\right\}\)
mà \(x\in Z\)nên \(3.\left(x-1\right)⋮3\)
Vậy \(3.\left(x-1\right)\in\left\{-6;-3;0;3;6\right\}\)
hay \(x-1\in\left\{-2;-1;0;1;2\right\}\)
tới đây dễ rồi thì làm nốt nhé, để thời gian làm mấy câu sau!
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình elip theo cú pháp x^2/10 + y^2/4 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
b) Nhập phương trình elip theo cú pháp x^2/12 + y^2/3 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
c) Nhập phương trình elip theo cú pháp x^2/100 + y^2/36 = 1 vào vùng nhập lệnh ta được hình elip dưới đây: