Năm bạn Nhân, Lễ, Nghĩa, Trí và Tín sắp xếp một cách ngẫu nhiên thành một hàng ngang để chụp ảnh. Tính xác suất của biến cố:
a) “Nhân và Tín không đứng cạnh nhau”
b) “Trí không đứng ở đầu hàng”
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tham khảo
A là biến cố "Cường đứng đầu hàng", \(P\left(A\right)=\dfrac{6!.C^1_2}{7!}=\dfrac{2}{7}\)
B là biến cố "Trọng đứng đầu hàng", \(P\left(B\right)=\dfrac{6!.C^1_2}{7!}=\dfrac{2}{7}\)
AB là biến cố "Trọng và Cường cùng đứng đầu hàng" \(P\left(AB\right)=\dfrac{2!.5!}{7!}=\dfrac{1}{21}\)
\(A\cup B\)
là biến cố "Có ít nhất một trong hai bạn Cường và Trọng đứng ở đầu hàng"
\(P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\right).P\left(B\right)=\dfrac{11}{21}\)
THAM KHẢO:
A là biến cố "Cường đứng đầu hàng", P(A)=\(\dfrac{6!.C\dfrac{1}{2}}{7!}=\dfrac{2}{7}\)
B là biến cố "Trọng đứng đầu hàng", P(B)=\(\dfrac{6!.C\dfrac{1}{2}}{7!}=\dfrac{2}{7}\)
AB là biến cố "Trọng và Cường cùng đứng đầu hàng" P(AB)=\(\dfrac{2!.5!}{7!}=\dfrac{1}{21}\)
A∪B là biến cố "Có ít nhất một trong hai bạn Cường và Trọng đứng ở đầu hàng"
P(A∪B)=P(A)+P(B)−P(A).P(B)=\(\dfrac{11}{21}\)

Chọn C
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố "không có hai học sinh nữ nào đứng cạnh nhau".
Mỗi phần tử của A tương ứng với 1 hàng ngang gồm 11 bạn đã cho mà không có hai nữ xếp cạnh nhau. Để xếp được 1 hàng như vậy ta thực hiện liên tiếp hai bước:
Bước 1: Xếp 6 bạn nam thành một hàng ngang, có 6!= 720 cách
Bước 2: Xếp 5 bạn nữ vào 7 vị trí xen giữa hai nam hoặc ngoài cùng (để 2 nữ không cạnh nhau), có A 7 5 = 2520 cách.
Vậy n(A) =720.2520 = 1814400
Xác suất cần tìm là 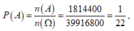

HD: Xếp 10 học sinh thành 1 hàng ngang có:
![]()
Gọi A là biến cố: “Hàng ngang không có 2 bạn nữ nào đứng cạnh nhau”
Sắp xếp 5 bạn nam thành 1 hàng có: 5! cách sắp xếp, khi đó có 6 vị trị để xếp 5 bạn nữ xen kẽ để không có hai bạn nữ đứng cạnh nhau (6 vị trí bao gồm 2 vị trí đầu và cuối và 4 vị trí giữa 2 bạn nam)
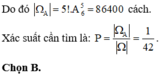

Cách 1:
n ( Ω ) = 10 !
Bước 1: Xếp 5 bạn nữ có: 5! Cách
Bước 2: Xếp 5 bạn nam vào xen giữa 4 khoảng trống của 5 bạn nữ và hai vị trí đầu hàng. Có hai trường hợp sau
+) TH1: Xếp 4 bạn nam vào 4 khoảng trống giữa 5 bạn nữ, bạn nam còn lại có hai lựa chọn:
Xếp vào hai vị trí đầu hàng. Trường hợp này có A 5 4 . 2 cách
+) TH2:
- Chọn một khoảng trống trong 4 khoảng trống giữa hai bạn nữ để xếp hai bạn nam có C 4 1 cách
- Chọn hai bạn nam trong 5 bạn nam để xếp vào vị trí đó có A 5 2 cách
- Ba khoảng trống còn lại xếp còn lại ba bạn nam còn lại có 3! Cách
Trường hợp này có C 4 1 . A 5 2 . 3 ! cách
Vậy có tất cả 5 ! ( A 5 4 . 2 + C 4 1 . A 5 2 . 3 ! ) cách
Vậy xác suất là: P = 5 ! ( A 5 4 . 2 + C 4 1 . A 5 2 . 3 ! ) 10 ! = 1 42
Cách 2:
n ( Ω ) = 10 !
- Xếp 5 bạn nam có 5! Cách
- Xếp 5 bạn nữ xen vào giữa 4 khoảng trống và 2 vị trí đầu hàng có A 6 5 cách
Vậy 5 ! . A 6 5 cách
Vậy P = 5 ! . A 6 5 10 ! = 1 42
Chọn đáp án B.

Chọn B
Số phần tử của không gian mẫu là ![]()
Sắp 5 học sinh nam thành một hàng ngang, có 5! cách (tạo ra khoảng trống).
Chọn 3 khoảng trống trong 6 khoảng trống để xếp 3 nữ, có C 6 3 cách chọn. Khi đó, số cách xếp 3 bạn nữ là C 6 3 .3! cách.
Vậy xác suất cần tìm là 

Đáp án B
Gọi a 1 , a 2 , a 3 là 3 ví trí chọn 3 người ⇒ 1 ≤ a 1 < a 2 < a 3 ≤ 12
Theo bài ra ta có a 1 < a 2 − 1 a 2 < a 3 − 1 ⇒ 1 ≤ a 1 < a 2 − 1 < a 3 − 2 ≤ 10
⇒ Có C 10 3 cách chọn bộ ba vị trí a 1 ; a 2 − 1 ; a 3 − 2
⇒ Có C 10 3 cách chọn bộ ba vị trí thỏa mãn yêu cầu bài toán
Vạy xác suất cần tính là P = C 10 3 C 12 3 = 6 11

Đáp án B
Có n ( Ω ) = C 12 3
Giả sử chọn 3 người có số thứ tự trong hàng lần lượt là a, b, c
Theo giả thiết ta có: a < b < c, b – a > 1, c – b > 1, a , b , c ∈ { 1 , 2 , . . . , 12 } .
Hhjj
Tổng số kết quả có thể xảy ra của phép thử là \(n(\Omega ) = 5!\)
a) Gọi biến cố A “Nhân và Tín đứng cạnh nhau” là biến cố đối của biến cố “Nhân và Tín không đứng cạnh nhau”
Số kết quả thuận lợi cho A là: \(n(A) = 2!.3!{.2^3}\)
Xác suất của biến cố A là: \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{2!.3!{{.2}^3}}}{{5!}} = \frac{4}{5}\)
Vậy xác suất của biến cố “Nhân và Tín không đứng cạnh nhau” là \(1 - \frac{4}{5} = \frac{1}{5}\)
b) Gọi biến cố A “Trí đứng ở đầu hàng” là biến cố đối của biến cố “Trí không đứng ở đầu hàng”
Số kết quả thuận lợi cho A là: \(n(A) = 4!.2\)
Xác suất của biến cố A là: \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{4!.2}}{{5!}} = \frac{2}{5}\)
Vậy xác suất của biến cố “Nhân và Tín không đứng cạnh nhau” là \(1 - \frac{2}{5} = \frac{3}{5}\)