Viết phương trình chính tắc của các đường conic dưới đây. Gọi tên và tìm tọa độ của các tiêu điểm của chúng
a) \(({C_1}):4{x^2} + 16{y^2} = 1\)
b) \(({C_2}):16{x^2} - 4{y^2} = 144\)
c) \(({C_3}):x = \frac{1}{8}{y^2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đây là một parabol. Tiêu điểm của parabol có tọa độ là: \(F\left({\frac{9}{2};0} \right)\).
b) Đây là một elip. Tiêu điểm của elip có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} - {b^2}} ;0} \right) = \left( { - \sqrt {39} ;0} \right)\\{F_2}\left( {\sqrt {{a^2} - {b^2}} ;0} \right) = \left( {\sqrt {39} ;0} \right)\end{array} \right.\)
c) Đây là một hyperbol. Tiêu điểm của hypebol có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} + {b^2}} ;0} \right) = \left( { - 5;0} \right)\\{F_2}\left( {\sqrt {{a^2} + {b^2}} ;0} \right) = \left( {5;0} \right)\end{array} \right.\)

a) Phương trình \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\) đã có dạng phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) nên ta có: \(a = 10,b = 6 \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt {{{10}^2} - {6^2}} = 8 \)
Suy ra ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 8;0} \right),{F_2}\left( {8;0} \right)\)
Tọa độ các đỉnh: \(A(0;6),B(10;0),C(0; - 6),D( - 10;0)\)
Độ dài trục lớn 20
Độ dài trục nhỏ 12
b) Phương trình \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\) đã có dạng phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) nên ta có: \(a = 5,b = 4 \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt {{5^2} - {4^2}} = 3\)
Suy ra ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 3;0} \right),{F_2}\left( {3;0} \right)\)
Tọa độ các đỉnh: \(A(0;4),B(5;0),C(0; - 4),D( - 5;0)\)
Độ dài trục lớn 10
Độ dài trục nhỏ 8
c) \({x^2} + 16{y^2} = 16 \Leftrightarrow \frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{1} = 1\)
Vậy ta có phương trình chính tắc của elip đã cho là \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{1} = 1\)
Suy ra \(a = 4,b = 1 \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt {{4^2} - {1^2}} = \sqrt {15} \)
Từ đó ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - \sqrt {15} ;0} \right),{F_2}\left( {\sqrt {15} ;0} \right)\)
Tọa độ các đỉnh: \(A(0;1),B(4;0),C(0; - 1),D( - 4;0)\)
Độ dài trục lớn 8
Độ dài trục nhỏ 2

a) Phương trình \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\) đã có dạng phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) nên ta có: \(a = 4,b = 3 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{4^2} + {3^2}} = 5\)
Suy ra ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\)
Tọa độ các đỉnh: \(A(0;3),B(4;0),C(0; - 3),D( - 4;0)\)
Độ dài trục thực 8
Độ dài trục ảo 6
b) Phương trình \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\) đã có dạng phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) nên ta có: \(a = 8,b = 6 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{8^2} + {6^2}} = 10\)
Suy ra ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 10;0} \right),{F_2}\left( {10;0} \right)\)
Tọa độ các đỉnh: \(A(0;6),B(8;0),C(0; - 6),D( - 8;0)\)
Độ dài trục thực 16
Độ dài trục ảo 12
c) \({x^2} - 16{y^2} = 16 \Leftrightarrow \frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{1} = 1\)
Vậy ta có phương trình chính tắc của hypebol đã cho là \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{1} = 1\)
Suy ra \(a = 4,b = 1 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{4^2} + {1^2}} = \sqrt {17} \)
Từ đó ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - \sqrt {17} ;0} \right),{F_2}\left( {\sqrt {17} ;0} \right)\)
Tọa độ các đỉnh: \(A(0;1),B(4;0),C(0; - 1),D( - 4;0)\)
Độ dài trục thực 8
Độ dài trục ảo 2
d) \(9{x^2} - 16{y^2} = 144 \Leftrightarrow \frac{{{x^2}}}{{\frac{{144}}{9}}} - \frac{{{y^2}}}{{\frac{{144}}{{16}}}} = 1\)
Vậy ta có phương trình chính tắc của hypebol đã cho là \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
Suy ra \(a = 4,b = 3 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{4^2} + {3^2}} = 5\)
Từ đó ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\)
Tọa độ các đỉnh: \(A(0;3),B(4;0),C(0; - 3),D( - 4;0)\)
Độ dài trục thực 8
Độ dài trục ảo 6

Từ phương trình chính tắc của (E) ta có: \(a = 7,b = 5 \Rightarrow c = 2\sqrt 6 {\rm{ }}(do{\rm{ }}{{\rm{c}}^2} + {b^2} = {a^2})\)
Vậy ta có tọa độ các giao điểm của (E) với trục Ox, Oy là: \({A_1}\left( { - 7;{\rm{ }}0} \right)\)\({A_2}\left( {7;{\rm{ }}0} \right)\)\({B_1}\left( {0; - {\rm{ 5}}} \right)\)\({B_2}\left( {0;{\rm{ 5}}} \right)\)
Hai tiêu điểm của (E) có tọa độ là: \({F_1}\left( { - 2\sqrt 6 ;0} \right),{F_2}\left( {2\sqrt 6 ;0} \right)\)

a:
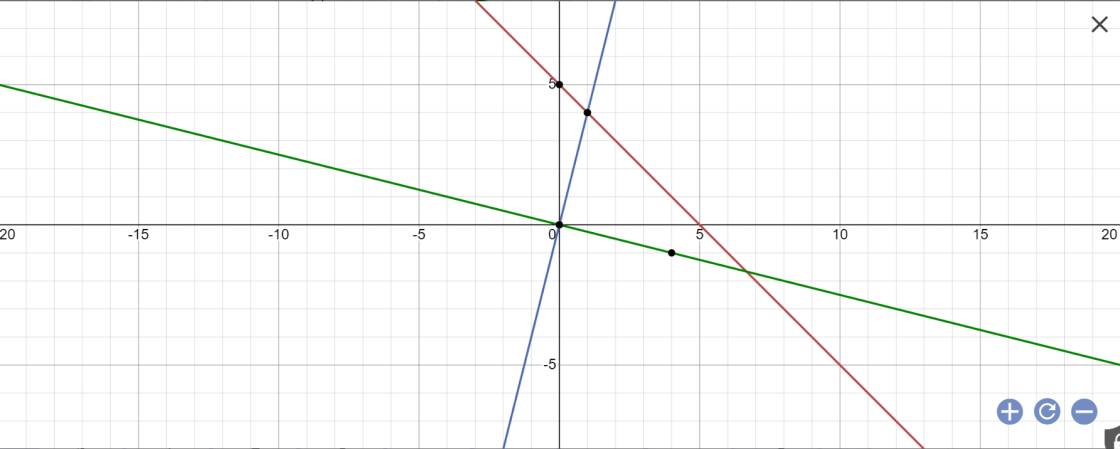
b: tọa độ A là;
-x+5=4x và y=4x
=>x=1 và y=4
Tọa độ B là;
-x+5=-1/4x và y=-1/4x
=>-3/4x=-5 và y=-1/4x
=>x=5:3/4=5*4/3=20/3 và y=-1/4*20/3=-5/3
=>B(20/3;-5/3)
c: O(0;0); A(1;4); B(20/3;-5/3)
\(OA=\sqrt{1^2+4^2}=\sqrt{17}\)
\(OB=\sqrt{\left(\dfrac{20}{3}\right)^2+\left(-\dfrac{5}{3}\right)^2}=\dfrac{5\sqrt{17}}{3}\)
\(AB=\sqrt{\left(\dfrac{20}{3}-1\right)^2+\left(-\dfrac{5}{3}-4\right)^2}=\dfrac{\sqrt{818}}{3}\)
\(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{-8}{17}\)
=>góc AOB tù
=>ΔOAB tù

a) Ta có: \(a = 3,b = 4 \Rightarrow c = \sqrt {{3^2} + {4^2}} = 5\)
Vậy tiêu điểm của (E) là: \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\)
b) Ta có: \(a = 6;b = 5 \Rightarrow c = \sqrt {{6^2} + {5^2}} = \sqrt {61} \)
Vậy tiêu điểm của (E) là: \({F_1}\left( { - \sqrt {61} ;0} \right),{F_2}\left( {\sqrt {61} ;0} \right)\)
a) Ta thấy phương trình có dạng \(a{x^2} + b{y^2} = 1\) nên phương trình \(({C_1}):4{x^2} + 16{y^2} = 1\) là phương trình của đường elip
Từ phương trình \(({C_1}):4{x^2} + 16{y^2} = 1\) ta có phương trình chính tắc là \(({C_1}):\frac{{{x^2}}}{{\frac{1}{4}}} + \frac{{{y^2}}}{{\frac{1}{{16}}}} = 1\)
Từ phương trình chính tắc ta có: \(a = \frac{1}{2},b = \frac{1}{4} \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt {{{\left( {\frac{1}{2}} \right)}^2} - {{\left( {\frac{1}{4}} \right)}^2}} = \frac{{\sqrt 3 }}{4}\)
Suy ra tiêu điểm của elip này là \({F_1}\left( { - \frac{{\sqrt 3 }}{4};0} \right)\) và \({F_2}\left( {\frac{{\sqrt 3 }}{4};0} \right)\)
b) Ta thấy phương trình có dạng \(a{x^2} - b{y^2} = 1\) nên phương trình \(({C_2}):16{x^2} - 4{y^2} = 144\) là phương trình của đường hypebol
Từ phương trình \(({C_2}):16{x^2} - 4{y^2} = 144\) ta có phương trình chính tắc là \(({C_1}):\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{36}} = 1\)
Từ phương trình chính tắc ta có: \(a = 3,b = 6 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{3^2} + {6^2}} = 3\sqrt 5 \)
Suy ra tiêu điểm của hypebol này là \({F_1}\left( { - 3\sqrt 5;0} \right)\) và \({F_2}\left( {3\sqrt 5;0} \right)\)
c) Phương trình \(({C_3}):x = \frac{1}{8}{y^2}\) có dạng \({y^2} = ax\) nên phương trình này là phương trình của parabol
Ta có phương trình chính tắc là \({y^2} = 8x\)
Từ phương trình chính tắc ta có: \(2p = 8 \Rightarrow p = 4\)
Suy ra tiêu điểm là \(F(2;0)\)