Một cổng chào có hình parabol cao 10 m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 2 2021
Do tính đối xứng của parabol, \(\Rightarrow H\) là trung điểm AB \(\Rightarrow y_H=y_A=y_B\) đồng thời \(x_A=-x_B\)
Mặt khác \(AB=\left|x_A-x_B\right|=\left|2x_A\right|=4\Rightarrow x_A=2\)
\(\Rightarrow y_A=-x_A^2=-4\Rightarrow y_H=-4\)
\(\Rightarrow OH=\left|y_H\right|=4\) (m)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
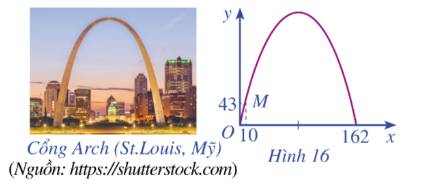
Từ đồ thị ta thấy các điểm thuộc đồ thị là: \(A\left( {0;0} \right),B\left( {10;43} \right),C\left( {162;0} \right)\).
Gọi hàm số là \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Thay tọa độ các điểm A, B, C vào ta được hệ:
\(\left\{ \begin{array}{l}a{.0^2} + b.0 + c = 0\\a{.10^2} + b.10 + c = 43\\a{.162^2} + b.162 + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}c = 0\\100a + 10b = 43\\{162^2}a + 162b = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}c = 0\\a = - \frac{{43}}{{1520}}\\b = \frac{{3483}}{{760}}\end{array} \right.\)
Từ đố ta có \(y = - \frac{{43}}{{1520}}{x^2} + \frac{{3483}}{{760}}x\)
Hoành độ đỉnh của đồ thị là: \(x = - \frac{b}{{2a}} = 81\)
Khi đó: \(y = - \frac{{43}}{{1520}}{.81^2} + \frac{{3483}}{{760}}.81 \approx 186\)(m)
Vậy chiều cao của cổng là 186m.
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
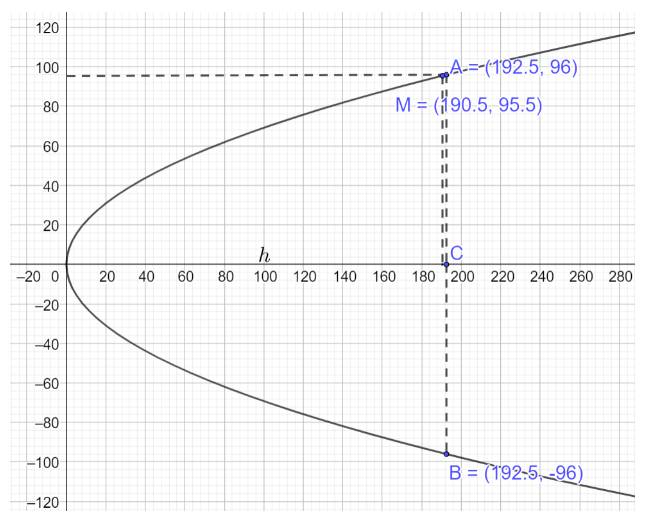
Phương trình parabol mô phỏng cổng có dạng \({y^2} = 2px\)
Theo giả thiết \(AB = 2{y_A} = 192 \Rightarrow {y_A} = 96,OC = h \Rightarrow M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\)
Thay tọa độ các điểm \(M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\) vào phương trình \({y^2} = 2px\) ta có:
\(\left\{ \begin{array}{l}95,{5^2} = 2p\left( {h - 2} \right)\\{96^2} = 2ph\end{array} \right. \Rightarrow \left\{ \begin{array}{l}p = \frac{{383}}{{16}}\\h \simeq 192,5\end{array} \right.\)
Vậy chiều cao của cổng gần bằng 192,5 m
Vẽ lại parabol và chọn hệ trục tọa độ như hình dưới
Gọi phương trình của parabol là \({y^2} = 2px\)
Ta có chiều cao của cổng \(OH = BK = 10\), chiều rộng tại chân cổng \(BD = 2BH = 5\)
Vậy điểm B có tọa độ là \(B\left( {10;\frac{5}{2}} \right)\)
Thay tọa độ điểm B vào phương trình parabol ta có:
\({\left( {\frac{5}{2}} \right)^2} = 2p.10 \Rightarrow p = \frac{5}{{16}}\), suy ra phương trình parabol có dạng \({y^2} = \frac{5}{8}x\)
Thay \(x = 2\) vào phương trình \({y^2} = \frac{5}{8}x\) ta tìm được \(y = \frac{{\sqrt 5 }}{2}\)
Vậy bề rộng của cổng tại chỗ cách đỉnh 2 m là \(\sqrt 5 \) m