Một trò chơi trên máy tính đang mô phỏng một vùng biển có hai hòn đảo nhỏ có tọa độ \(B\left( {50;30} \right)\) và \(C\left( {32; - 23} \right)\). Một con tàu đang neo đậu tại điểm \(A\left( { - 10;20} \right)\)a) Tính số đo của \(\widehat {BAC}\)b) Cho biết một đơn vị trên hệ trục tọa độ tương ứng với 1km. Tính khoảng cách từ con tàu đến mỗi hòn...
Đọc tiếp
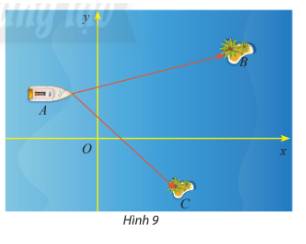
Một trò chơi trên máy tính đang mô phỏng một vùng biển có hai hòn đảo nhỏ có tọa độ \(B\left( {50;30} \right)\) và \(C\left( {32; - 23} \right)\). Một con tàu đang neo đậu tại điểm \(A\left( { - 10;20} \right)\)
a) Tính số đo của \(\widehat {BAC}\)
b) Cho biết một đơn vị trên hệ trục tọa độ tương ứng với 1km. Tính khoảng cách từ con tàu đến mỗi hòn đảo
a) Ta có: \(\overrightarrow {AB} = \left( {60;10} \right),\overrightarrow {AC} = \left( {42; - 43} \right),\overrightarrow {BC} = \left( { - 18; - 53} \right)\)
\(\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} = \frac{{60.42 + 10.( - 43)}}{{\sqrt {{{60}^2} + {{10}^2}} .\sqrt {{{42}^2} + {{\left( { - 43} \right)}^2}} }} \simeq 0,572 \Rightarrow \widehat {BAC} \approx 55^\circ 8'\)
b)
Khoảng cách từ tàu đến đảo B là \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{60}^2} + {{10}^2}} = 10\sqrt {37} \) (km)
Khoảng cách từ tàu đến đảo B là \(AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{{42}^2} + {{\left( { - 43} \right)}^2}} = \sqrt {3613} \) (km)