Một chú cá heo nhảy lên khỏi mặt nước sau t giây được cho bởi hàm số \(h\left( t \right) = - 4,9{t^2} + 9,6t\)
Tính khoảng thời gian cá heo ở trên không.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để quả bóng ở độ cao trên 5m so với mặt đất thì:
\(\begin{array}{l}h(t) > 5\\ \Rightarrow - 4,9{t^2} + 20t + 1 > 5\\ \Rightarrow - 4,9{t^2} + 20t - 4 > 0\end{array}\)
Đặt \(f(t) = - 4,9{t^2} + 20t - 4\)có \(\Delta ' = b{'^2} - ac = {10^2} - ( - 4,9).( - 4) = 80,4 > 0\)nên \(f(t)\)có 2 nghiệm: \(\begin{array}{l}{t_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a} = \frac{{ - 10 + \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 - \sqrt {80,4} }}{{4,9}}\\{t_2} = \frac{{ - b' - \sqrt {\Delta '} }}{a} = \frac{{ - 10 - \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 + \sqrt {80,4} }}{{4,9}}\end{array}\)
Mặt khác \(a = - 4,9 < 0\), do đó ta có bảng xét dấu sau

Do đó để \(h(t) > 5\)thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\)
Vậy để quả bóng sẽ ở độ cao trên 5m so với mặt đất thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\)

Theo giả thiết, khoảng thời gian bóng nằm ở độ cao 40 m là nghiệm của bất phương trình sau:
\(\begin{array}{l}h\left( t \right) > 40 \Leftrightarrow - 4,9{t^2} + 30t + 2 > 40\\ \Leftrightarrow - 4,9{t^2} + 30t - 38 > 0\end{array}\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 30t - 38\) có \(\Delta = 155,2 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,8;{x_2} \simeq 4,3\) và có \(a = - 4,9 < 0\)
Ta có bảng xét dấu như sau:
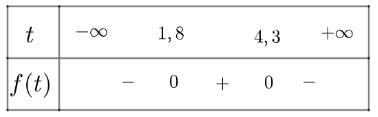
Từ đó cho thấy khoảng từ 1,8 s đến 4,3 s lag khoảng thời gian bóng cao so với mặt đất lớn hơn 40 m
Vậy quả bóng nằm ở độ cao trên 40 m trong thời gian 2,5 giây.

Đêm trắng , biển yên tĩnh. Một số chiến sĩ thả câu. Một số khác quây quần trên bông tàu ca hát , thổi sáo . Bỗng có tiếng đập nước ùm ùm như có ai đang tập bơi. Một người kêu lên “Cá heo[! ]“Anh em ùa ra vỗ tay hoan hô : A[! ]Cá heo nhảy múa đẹp quá[! ]“ Thế là cá thích , nhảy vút lên thật cao .Có chú quá đà , vọt lên boong tàu cách mặt nước đến một mét . Có lẽ va vào sắt bị đau , chú nằm im , mắt nhắm nghiền . Một anh chiến sĩ đên nâng con cá lên hai tay , nói nựng :
- Có đau không , chú mình[? ]Lần sau khi nhảy múa, phải chú ý nhé [ !]
Anh vuốt ve con cá rồi thả xuống nước. Cả đàn cá quay ngang lại phía boong tàu , nhảy vung lên một cái như để cảm ơn rồi tỏa ra biển rộng .

a) Theo giả thiết ta có bất phương trình sau: \( - 4,9{t^2} + 10t + 1,6 > 7 \Leftrightarrow - 4,9{t^2} + 10t - 5,4 > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 10t - 5,4\) có \(\Delta = - \frac{{146}}{{25}} < 0\) và \(a = - 4,9 < 0\)
nên \(f\left( x \right)\) âm với mọi t, suy ra bât phương trình \( - 4,9{t^2} + 10t + 1,6 > 7\) vô nghiệm
vậy bóng không thể cao trên 7 m
b) Theo giả thiết ta có bất phương trình sau: \( - 4,9{t^2} + 10t + 1,6 > 5 \Leftrightarrow - 4,9{t^2} + 10t - 3,4 > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 10t - 3,4\) có hai nghiệm phân biệt là \({t_1} \simeq 0,43;{t_2} \simeq 1,61\) và \(a = - 4,9 < 0\)
nên \(f\left( t \right)\) dương khi t nằm trong khoảng \(\left( {0,43;1,61} \right)\)
Vậy khi t nằm trong khoảng \(\left( {0,43;1,61} \right)\)giây thì bóng ở độ cao trên 5 m

a)
\(\begin{array}{l}\begin{array}{*{20}{l}}{\left[ {5;5,1} \right]}\end{array}:t = 5,1 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{1^2} - 4,{{9.5}^2}}}{{5,1 - 5}} = 49,49\\\begin{array}{*{20}{l}}{\left[ {5;5,05} \right]}\end{array}:t = 5,05 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{05}^2} - 4,{{9.5}^2}}}{{5,05 - 5}} = 49,245\\\begin{array}{*{20}{l}}{\left[ {5;5,01} \right]}\end{array}:t = 5,01 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{01}^2} - 4,{{9.5}^2}}}{{5,01 - 5}} = 49,049\\\begin{array}{*{20}{l}}{\left[ {5;5,001} \right]}\end{array}:t = 5,001 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{001}^2} - 4,{{9.5}^2}}}{{5,001 - 5}} = 49,0049\\\begin{array}{*{20}{l}}{\left[ {4,999;5} \right]}\end{array}:t = 4,999 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.4,{{999}^2} - 4,{{9.5}^2}}}{{4,999 - 5}} = 48,9951\\\begin{array}{*{20}{l}}{\left[ {4,99;5} \right]}\end{array}:t = 4,99 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.4,{{99}^2} - 4,{{9.5}^2}}}{{4,99 - 5}} = 48,951\end{array}\)

Ta thấy: \(\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}\) càng gần 49 khi \(t\) càng gần 5.
b)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to 5} \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9{t^2} - 4,{{9.5}^2}}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {{t^2} - {5^2}} \right)}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {t - 5} \right)\left( {t + 5} \right)}}{{t - 5}}\\ = \mathop {\lim }\limits_{t \to 5} 4,9\left( {t + 5} \right) = 4,9\left( {5 + 5} \right) = 49\end{array}\)
c)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to {t_0}} \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9{t^2} - 4,9.t_0^2}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {{t^2} - t_0^2} \right)}}{{t - t_0^2}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {t - {t_0}} \right)\left( {t + {t_0}} \right)}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to 5} 4,9\left( {t + {t_0}} \right) = 4,9\left( {{t_0} + {t_0}} \right) = 9,8{t_0}\end{array}\)

a) Số nhiệt của thành phố A là:
\(I=-45+2\cdot40+10\cdot100-0,2\cdot40\cdot100-0,007\cdot40^2-0,05\cdot100^2+0,001\cdot40^2\cdot100+0,009\cdot40\cdot100^2-0,000002\cdot40^2\cdot100^2\)
\(I=-3345,2\)
b) Số nhiệt của thành phố B là:
\(I=-45+2\cdot50+10\cdot90-0,007\cdot50^2-0,05\cdot90^2+0,001\cdot50^2\cdot90+0,009\cdot50\cdot90^2-0,00000\cdot50^2\cdot90^2\)
\(I=-3780\)
a) Số nhiệt của thành phố A là:
b) Số nhiệt của thành phố B là:

Ta có: \(v\left(t\right)=h'\left(t\right)=-9,8t\)
a, Vận tốc của vật tại thời điểm t = 5s là \(v\left(5\right)=-9,8\cdot5=-49\left(m/s\right)\)
b, Khi vật chạm đất thì \(h\left(t\right)=100-4,9t^2=0 \Rightarrow t=\dfrac{10\sqrt{10}}{7}\left(s\right)\)
Khi đó, vận tốc vật chạm đất là: \(v\left(\dfrac{10\sqrt{10}}{7}\right)=-9,8\cdot\dfrac{10\sqrt{10}}{7}=-14\sqrt{10}\left(m/s\right)\)
Khoảng thời gian cá heo ở trên không chính khoảng cá heo cao hơn mặt nước
Ta có bất phương trình \(h\left( t \right) > 0 \Leftrightarrow - 4,9{t^2} + 9,6t > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 9,6t\) có \(\Delta = 92.16 > 0\), có hai nghiệm phân biệt là \({x_1} = 0,{x_2} = \frac{{96}}{{49}}\) và có \(a = - 4,9 < 0\)
Ta có bảng xét dấu như sau:
Vậy khoảng thời gian cá heo ở trên không là khoảng \(\left( {0;\frac{{96}}{{49}}} \right)\) giây