Cho 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đều khác vectơ \(\overrightarrow 0 \). Các khẳng định sau đúng hay sai?a) Nếu hai vectơ \(\overrightarrow a ,\overrightarrow b \) cùng phương với \(\overrightarrow c \) thì \(\overrightarrow a \) và \(\overrightarrow b \) cùng phươngb) Nếu hai vectơ \(\overrightarrow a ,\overrightarrow b \) cùng ngược hướng với \(\overrightarrow c \) thì \(\overrightarrow a \) và \(\overrightarrow b \) cùng...
Đọc tiếp
Cho 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đều khác vectơ \(\overrightarrow 0 \). Các khẳng định sau đúng hay sai?
a) Nếu hai vectơ \(\overrightarrow a ,\overrightarrow b \) cùng phương với \(\overrightarrow c \) thì \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương
b) Nếu hai vectơ \(\overrightarrow a ,\overrightarrow b \) cùng ngược hướng với \(\overrightarrow c \) thì \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng
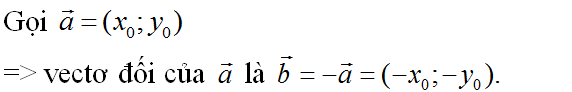
a)
+) Vectơ \(\overrightarrow a \) cùng phương với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow a \) song song với giá của vectơ \(\overrightarrow c \)
+) Vectơ \(\overrightarrow b \) cùng phương với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow b \) song song với giá của vectơ \(\overrightarrow c \)
Suy ra giá của vectơ \(\overrightarrow a \) và vectơ \(\overrightarrow b \) song song với nhau nên \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương
Vậy khẳng định trên đúng
b) Giả sử vectơ \(\overrightarrow c \) có hướng từ A sang B
+) Vectơ \(\overrightarrow a \) ngược hướng với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow a \) song song với giá của vectơ \(\overrightarrow c \) và có hướng từ B sang A
+) Vectơ \(\overrightarrow b \) ngược hướng với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow b \) song song với giá của vectơ \(\overrightarrow c \) và có hướng từ B sang A
Suy ra, hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng
Vậy khẳng định trên đúng