Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \); \(\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} = \overrightarrow {DC} \)
Mà ABCD là hình thang nên AB//DC. Mặt khác vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \) đều có hướng từ trái sang phải, suy ra vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \)cùng hướng
Vậy hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
a) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} \\= \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) \\= \overrightarrow 0 + 2\overrightarrow {MN} + \overrightarrow 0 = 2\overrightarrow {MN} \) (đpcm)
b) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
\(\)\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} \)
\(\left( {\overrightarrow {BM} + \overrightarrow {AM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) = 2\overrightarrow {MN} \)
Mặt khác ta có: \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \)
Suy ra \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
Cách 2:
\(\begin{array}{l}
\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \\
\Leftrightarrow \overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BC} - \overrightarrow {BD} \\
\Leftrightarrow \overrightarrow {DC} = \overrightarrow {DC} (đpcm)
\end{array}\)
a)
Kẻ BD.
Trong tam giác ABD có MQ là đường trung bình nên MQ//BD và \(MQ=\dfrac{1}{2}BD\). (1)
Trong tam giác CBD có PN là đường trung bình nên PN//BD và \(NP=\dfrac{1}{2}BD\). (2)
Từ (1) và (2) suy ra: \(\overrightarrow{MQ}=\overrightarrow{NP}\).
Kẻ AC.
Trong tam giác ABC có MN là đường trung bình suy ra:
NM//CA và \(NM=\dfrac{1}{2}CA\). (3)
Trong tam giác DAC có PQ là đường trung bình nên:
PQ//AC và \(PQ=\dfrac{1}{2}CA\). (4)
Từ (3) và (4) suy ra: \(\overrightarrow{PQ}=\overrightarrow{NM}\).
Dễ thấy:
\(AD = BC\) nhưng \(AD\) và \(BC\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) không bằng nhau.
\(CD > AB\) do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không bằng nhau.
\(AC\) và \(BD\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) không bằng nhau.
a)
MN là đường trung bình của tam giác ABC nên \(\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{AC}\).
QP là đường trung bình của tam giác ABC nên \(\overrightarrow{QP}=\dfrac{1}{2}\overrightarrow{AC}\).
Vậy \(\overrightarrow{MN}=\overrightarrow{QP}\).
b) Giả sử:
\(\overrightarrow{MP}=\overrightarrow{MN}+\overrightarrow{MQ}\Leftrightarrow\overrightarrow{MP}-\overrightarrow{MN}-\overrightarrow{MQ}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MP}+\overrightarrow{NM}+\overrightarrow{QM}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{QM}+\overrightarrow{MP}\right)+\overrightarrow{NM}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}+\overrightarrow{NM}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}-\overrightarrow{MN}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}-\overrightarrow{QP}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{0}=\overrightarrow{0}\) ( Điều giả sử đúng).
Vậy \(\overrightarrow{MP}=\overrightarrow{MN}+\overrightarrow{MQ}.\)
Ta có:
\(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} \)
Mặt khác: \(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \)
\(\begin{array}{l} \Rightarrow 2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} + \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \\ \Leftrightarrow 2\overrightarrow {MN} = \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {DN} + \overrightarrow {CN} } \right) + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow {BC} + \overrightarrow {AD} \end{array}\)
Lại có:
\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BD} + \overrightarrow {DC} + \overrightarrow {AD} = \overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {BD} = \overrightarrow {AC} + \overrightarrow {BD} .\)
Vậy \(\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \;\overrightarrow {AC} + \overrightarrow {BD} .\)
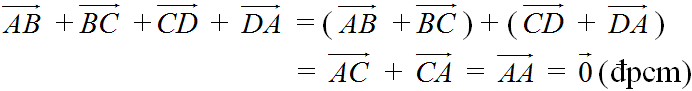
a) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DA} } \right) = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow {AA} = \overrightarrow 0 \)
b) \(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DA} + \overrightarrow {AB} = \overrightarrow {DB} \)
c) \(\overrightarrow {CB} - \overrightarrow {CD} = \overrightarrow {CB} + \overrightarrow {DC} = \overrightarrow {DC} + \overrightarrow {CB} = \overrightarrow {DB} \)