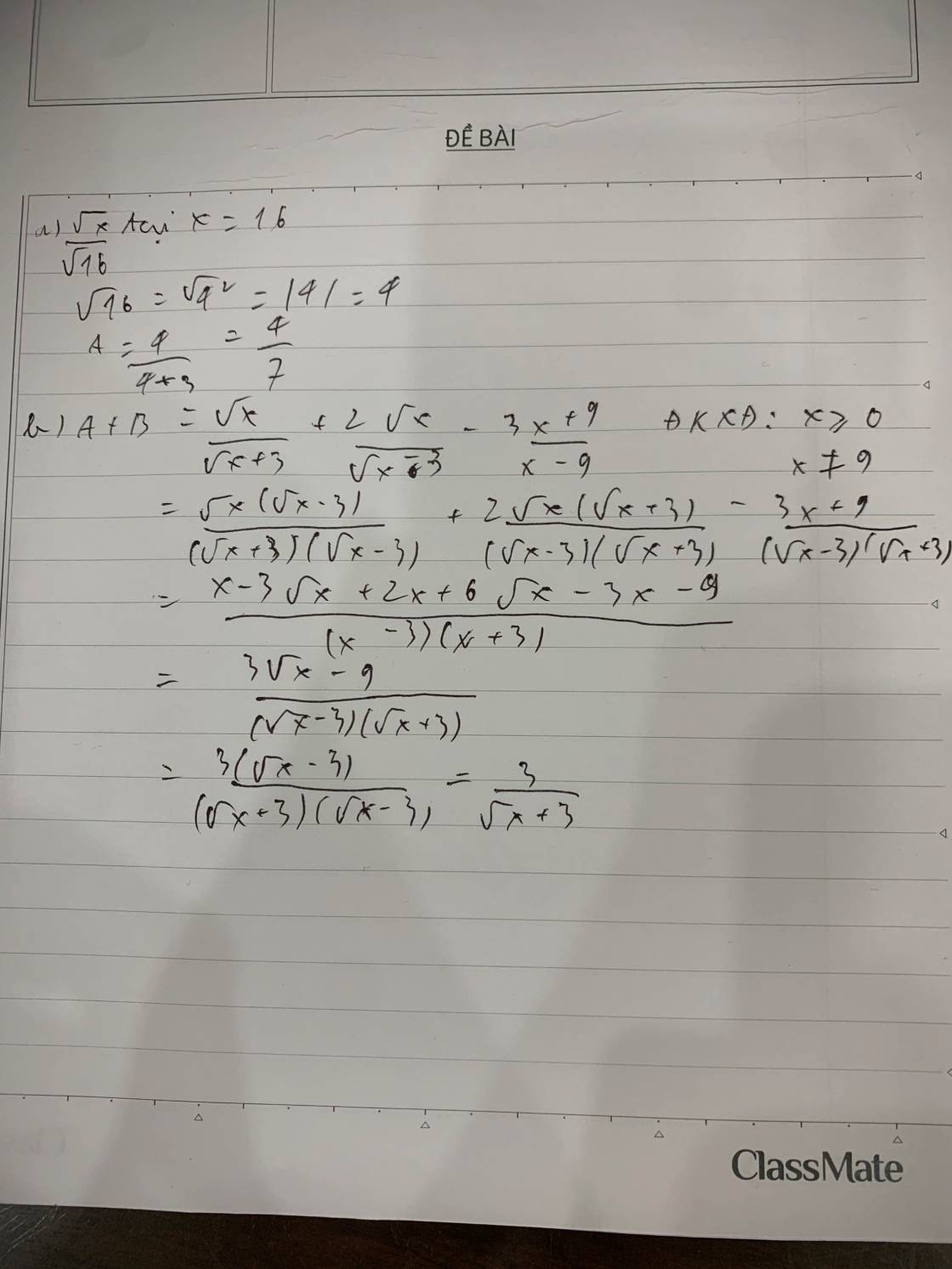Cho hai biểu thức: P = (sqrt(x - 2))/(sqrt(x) - 3) và Q = √x 6√x + 3 √x-3 9-x √x+3 (với x>0; x#9) a) Tính giá trị của P khi x = 9 . b) Rút gọn Q. c) Tìm x để biểu thức A = P.Q đạt giá trị nhỏ nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NC
29 tháng 8 2020
Bài làm:
Ta có:
\(P=\left(1-\frac{x-3\sqrt{x}}{x-9}\right)\div\left(\frac{\sqrt{x}-9}{2-\sqrt{x}}+\frac{\sqrt{x}-2}{3+\sqrt{x}}-\frac{9-x}{x+\sqrt{x}-6}\right)\)
\(P=\frac{x-9-x+3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\div\left[\frac{\left(9-\sqrt{x}\right)\left(3+\sqrt{x}\right)+\left(\sqrt{x}-2\right)^2-9+x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\right]\)
\(P=\frac{3\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\div\frac{-x+6\sqrt{x}+27+x-4\sqrt{x}+2-9+x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(P=\frac{3}{\sqrt{x}+3}\div\frac{x+2\sqrt{x}+20}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(P=\frac{3}{\sqrt{x}+3}\cdot\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}{x+2\sqrt{x}+20}\)
\(P=\frac{3\left(\sqrt{x}-2\right)}{x+2\sqrt{x}+20}=\frac{3\sqrt{x}-6}{x+2\sqrt{x}+20}\)
B
15 tháng 5 2021
Bài làm :
1) Khi x=9 ; giá trị của A là :
\(A=\frac{\sqrt{9}}{\sqrt{9}+2}=\frac{3}{3+2}=\frac{3}{5}\)
2) Ta có :
\(B=...\)
\(=\frac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\frac{1.\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\frac{1.\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x+2}\right)}\)
\(=\frac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{\sqrt{x}}{\sqrt{x}-2}\)
3) Ta có :
\(\frac{A}{B}=\frac{\sqrt{x}}{\sqrt{x}+2}\div\frac{\sqrt{x}}{\sqrt{x}-2}=\frac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\sqrt{x}}=\frac{\sqrt{x}-2}{\sqrt{x}+2}=\frac{\sqrt{x}+2-4}{\sqrt{x}+2}=1-\frac{4}{\sqrt{x}+2}\)
Xét :
\(\frac{A}{B}+1=\frac{4}{\sqrt{x+2}}>0\Rightarrow\frac{A}{B}>-1\)
=> Điều phải chứng minh
4 tháng 6 2021
1, thay x=9(TMĐKXĐ) vào A ta đk:
A=\(\dfrac{\sqrt{9}}{\sqrt{9}-2}=3\)
vậy khi x=9 thì A =3
2,với x>0,x≠4 ta đk:
B=\(\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
vậy B=\(\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
3,\(\dfrac{A}{B}>-1\) (x>0,x≠4)
⇒\(\dfrac{\sqrt{x}}{\sqrt{x}+2}:\dfrac{\sqrt{x}}{\sqrt{x}-2}>-1\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}+2}.\dfrac{\sqrt{x}-2}{\sqrt{x}}>-1\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}+2}>-1\)
⇒\(\sqrt{x}-2>-1\) (vì \(\sqrt{x}+2>0\))
⇔\(\sqrt{x}>1\)⇔x=1 (TM)
vậy x=1 thì \(\dfrac{A}{B}>-1\) với x>0 và x≠4
18 tháng 8 2020
Bài 1: Sửa đề: \(B=\left(\frac{x-2}{x+2\sqrt{x}}+\frac{1}{\sqrt{x}+2}\right)\cdot\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
a) Thay x=49 vào biểu thức \(A=\frac{\sqrt{x}+3}{\sqrt{x}-1}\), ta được:
\(A=\frac{\sqrt{49}+3}{\sqrt{49}-1}=\frac{7+3}{7-1}=\frac{10}{6}=\frac{5}{3}\)
Vậy: Khi x=49 thì \(A=\frac{5}{3}\)
b) Sửa đề: Rút gọn biểu thức B
Ta có: \(B=\left(\frac{x-2}{x+2\sqrt{x}}+\frac{1}{\sqrt{x}+2}\right)\cdot\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\left(\frac{x-2}{\sqrt{x}\left(\sqrt{x}+2\right)}+\frac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\right)\cdot\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\frac{x+\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)}\cdot\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\frac{x+2\sqrt{x}-\sqrt{x}-2}{\sqrt{x}\cdot\left(\sqrt{x}+2\right)}\cdot\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+2\right)-\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}\cdot\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\frac{\sqrt{x}+1}{\sqrt{x}}\)
c) Ta có: \(\frac{B}{A}=\frac{\sqrt{x}+1}{\sqrt{x}}:\frac{\sqrt{x}+3}{\sqrt{x}-1}\)
\(=\frac{\sqrt{x}+1}{\sqrt{x}}\cdot\frac{\sqrt{x}-1}{\sqrt{x}+3}\)
\(=\frac{x-1}{\sqrt{x}\left(\sqrt{x}+3\right)}\)
Để \(\frac{B}{A}< \frac{3}{4}\) thì \(\frac{x-1}{\sqrt{x}\left(\sqrt{x}+3\right)}-\frac{3}{4}< 0\)
\(\Leftrightarrow\frac{4\left(x-1\right)-3\sqrt{x}\left(\sqrt{x}+3\right)}{4\sqrt{x}\left(\sqrt{x}+3\right)}< 0\)
mà \(4\sqrt{x}\left(\sqrt{x}+3\right)>0\forall x\) thỏa mãn ĐKXĐ
nên \(4\left(x-1\right)-3\sqrt{x}\left(\sqrt{x}+3\right)< 0\)
\(\Leftrightarrow4x-4-3x-9\sqrt{x}< 0\)
\(\Leftrightarrow x-9\sqrt{x}-4< 0\)
\(\Leftrightarrow x^2-9x-4< 0\)
\(\Leftrightarrow x^2-2\cdot x\cdot\frac{9}{2}+\frac{81}{4}-\frac{97}{4}< 0\)
\(\Leftrightarrow\left(x-\frac{9}{2}\right)^2< \frac{97}{4}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-\frac{9}{2}>-\frac{\sqrt{97}}{2}\\x-\frac{9}{2}< \frac{\sqrt{97}}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>\frac{9-\sqrt{97}}{2}\\x< \frac{9+\sqrt{97}}{2}\end{matrix}\right.\)
Kết hợp ĐKXĐ, ta được:
\(3< x< \frac{9+\sqrt{97}}{2}\)
HS
1 tháng 8 2018
a, Rút gọn P
\(\dfrac{3}{\sqrt{x}+3}-\left(\dfrac{3-\sqrt{x}}{\sqrt{x}-2}+\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{2-\sqrt{x}}{\sqrt{x}+3}\right)\)
\(\Leftrightarrow\left(1-\dfrac{\sqrt{x}\left(\sqrt{x-3}\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}+3\right)}\right):\left(\dfrac{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}{x+3\sqrt{x}-2\sqrt{x}-6}-\dfrac{\sqrt{x}-3}{-\left(\sqrt{x}-2\right)\sqrt{x}+3}\right)\)
\(\Leftrightarrow\left(1-\dfrac{\sqrt{x}}{\sqrt{x}+3}\right):\left(\dfrac{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}{\sqrt{x}\left(\sqrt{x}+3\right)}+\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{2-\sqrt{x}}{\sqrt{x}+3}\right)\)
\(\Leftrightarrow\dfrac{3}{\sqrt{x}+3}:\left(\dfrac{3-\sqrt{x}}{\sqrt{x}-2}+\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{2-\sqrt{x}}{\sqrt{x}+3}\right)\)
\(\Leftrightarrow\dfrac{3}{\sqrt{x}+3}:\dfrac{\left(\sqrt{x}+3\right).\left(3-\sqrt{x}\right).\left(x+\sqrt{3}\right).\left(\sqrt{x}-3\right)-\left(\sqrt{x}-2\right).\left(2-\sqrt{x}\right)}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+3\right)}\)
\(\Leftrightarrow\dfrac{3}{\sqrt{x}+3}:\dfrac{\left(3+\sqrt{x}\right).\left(3-\sqrt{x}\right)+x-9-\left(2\sqrt{x}-x-4+2\sqrt{x}\right)}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+3\right)}\)
\(\Leftrightarrow\dfrac{3}{\sqrt{x}+3}:\dfrac{9-x+x-9-\left(4\sqrt{x}-x-4\right)}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+3\right)}\)
\(\Leftrightarrow\dfrac{3}{\sqrt{x}+3}:\dfrac{-4\sqrt{x}+x+4}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+3\right)}\)
\(\Leftrightarrow\dfrac{3}{\sqrt{x}+3}:\dfrac{x-4\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(\Leftrightarrow\dfrac{3}{\sqrt{x}+3}:\dfrac{\left(\sqrt[]{x}-2\right)^2}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+3\right)}\)
\(\Leftrightarrow\dfrac{3}{\sqrt{x}+3}:\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\)
\(\Leftrightarrow\dfrac{3}{\sqrt{x}+3}.\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(\Leftrightarrow3.\dfrac{1}{\sqrt{x}-2}\)
\(\Leftrightarrow\)\(\dfrac{3}{\sqrt{x}-2}\)
9 tháng 5 2022
1, Thay x = 16 vào ta được \(A=\dfrac{4}{4+3}=\dfrac{4}{7}\)
2, \(A+B=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{x-9}=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{-x+6\sqrt{x}-9}{x-9}=\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}-3}{\sqrt{x}+3}=\dfrac{3}{\sqrt{x}+3}\)
Ta có đpcm
