a) Cho điểm M là trung điểm của đoạn thẳng AB. Ta đã biết \(\overrightarrow {MB} = - \overrightarrow {MA} = \overrightarrow {AM} .\) Hoàn thành phép cộng vectơ sau: \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MA} + \overrightarrow {AM} = \overrightarrow {MM} = ?\)

b) Cho điểm G là trọng tâm của tam giác ABC có trung tuyến AI. Lấy D là điểm đối xứng với G qua I. Ta có BGCD là hình bình hành và G là trung điểm của đoạn thẳng AD. Với lưu ý rằng \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GD} \) và \(\overrightarrow {GA} = \overrightarrow {DG} \), hoàn thành các phép cộng vectơ sau:
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} + \overrightarrow {GD} = \overrightarrow {{\rm{DD}}} = ?\)

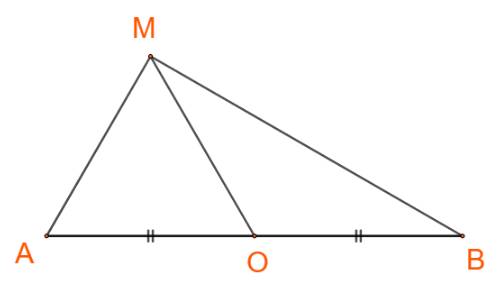

a) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MA} + \overrightarrow {AM} = \overrightarrow {MM} = \overrightarrow 0 \) (vì vectơ \(\overrightarrow {MB} = - \overrightarrow {MA} = \overrightarrow {AM} .\))
b) Xét hình bình hành BGCD ta có: \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GD} \)
\( \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} + \overrightarrow {GD} = \overrightarrow {DG} + \overrightarrow {GD} = \overrightarrow {{\rm{DD}}} = \overrightarrow 0 \)
(vì \(\overrightarrow {GA} = - \overrightarrow {GD} = \overrightarrow {DG} \))