Cho bất phương trình \(2x - y + 1 < 0\)
a) Vẽ đường thẳng \(y = 2x + 1\)
b) Các cặp số \(( - 2;0),(0;0),(1;1)\) có là nghiệm của bất phương trình đã cho không?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
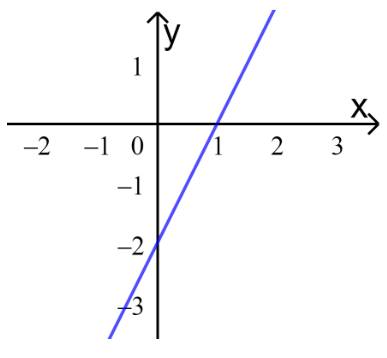
a) Cho \(x=0\Rightarrow y=-2\)
Cho \(y=0\Rightarrow x=1\)
Nối hai điểm (0;-2) và (1;0) ta được:
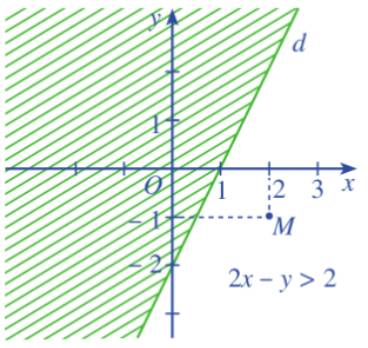
b) Thay tọa độ điểm M vào bất phương trình (3) ta được:
\(2.2 - \left( { - 1} \right) > 2 \Leftrightarrow 5 > 2\)(Luôn đúng)
Vậy (2;-1) là một nghiệm của bất phương trình (3)
c) Ta gạch đi nửa mặt phẳng không chứa M được:
6 tháng 10 2023
Câu a (-7;1)
Thay (-7;1) vào pt,ta có:
2.(-7) - 3.1 - 1 < 0
(=) -18<0
=> (-7;1) là nghiệm của bpt
6 tháng 10 2023
\(2x-3y-1< 0\left(d\right)\)
\(\left(-7;1\right)\in\left(d\right)\Leftrightarrow2.\left(-7\right)-3.1-1=-18< 0\left(đúng\right)\)
\(\left(0;-2\right)\in\left(d\right)\Leftrightarrow2.0-3.\left(-2\right)-1=5< 0\left(sai\right)\)
\(\rightarrow Chọn\) \(a\)
CM
13 tháng 11 2017
a) Cặp số (1; 1) là nghiệm của phương trình 2x – y = 1 vì 2.1 – 1 = 1
Cặp số (0,5; 0) là nghiệm của phương trình 2x – y = 1 vì 2.0,5 – 0 = 1
b) Chọn x = 2 ta có: 2.2 – y = 1 ⇔ y = 3
Vậy cặp số (2; 3) là một nghiệm của phương trình 2x – y = 1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2023
A là giao điểm AB và AC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}2x+y-4=0\\x-y+1=0\end{matrix}\right.\) \(\Rightarrow A\left(1;2\right)\)
Do B thuộc AB nên tọa độ có dạng: \(B\left(b;4-2b\right)\)
Do C thuộc AC nên tọa độ có dạng: \(C\left(c;c+1\right)\)
Áp dụng công thức trọng tâm:
\(\left\{{}\begin{matrix}1+b+c=3.2\\2+4-2b+c+1=3.1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b+c=5\\-2b+c=-4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=3\\c=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}B\left(3;-2\right)\\C\left(2;3\right)\\\end{matrix}\right.\)
Tham khảo:
a) Đường thẳng \(y = 2x + 1\) đi qua điểm \(A(0;1)\) và \(B\left( { - \frac{1}{2};0} \right)\)
b)
Vì \(2.( - 2) - 0 + 1 = - 3 < 0\)nên \(( - 2;0)\) là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Vì \(2.0 - 0 + 1 = 1 > 0\)nên \((0;0)\) không là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Vì \(2.1 - 1 + 1 = 2 > 0\)nên \(( - 2;0)\) không là nghiệm của bất phương trình \(2x - y + 1 < 0\)