Cho vectơ \(\overrightarrow a \ne \overrightarrow 0 \). Chứng minh rằng \(\frac{1}{{|\overrightarrow a |}}\;\overrightarrow a \) (hay còn được viết là \(\frac{{\overrightarrow a }}{{|\overrightarrow a |}}\)) là một vectơ đơn vị, cùng hướng với vectơ \(\overrightarrow a \).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
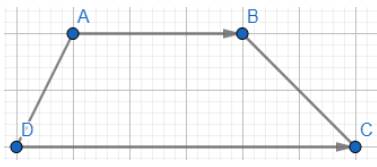
Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \); \(\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} = \overrightarrow {DC} \)
Mà ABCD là hình thang nên AB//DC. Mặt khác vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \) đều có hướng từ trái sang phải, suy ra vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \)cùng hướng
Vậy hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Tập hợp tất cả những điểm M để \(\overrightarrow {AM} \) vuông góc với \(\overrightarrow n \) là đường thẳng qua A và vuông góc với giá của vectơ \(\overrightarrow n \).
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
Để hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) (\(\overrightarrow v \ne 0\) ) cùng phương thì phải tồn tại một số \(k\left( {k \in \mathbb{R}} \right)\) sao cho \(\overrightarrow u = k.\overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = k{x_2}\\{y_1} = k{y_2}\end{array} \right.\) ( ĐPCM)
AH
Akai Haruma
Giáo viên
15 tháng 8 2021
Lời giải:
Xét hai vecto bất kỳ \(\overrightarrow{AB}, \overrightarrow{CD}\). Kẻ vecto $\overrightarrow{CT}$ sao cho $\overrightarrow{CT}=\overrightarrow{BA}$
Ta có:
\(|\overrightarrow{AB}+\overrightarrow{CD}|=|\overrightarrow{TC}+\overrightarrow{CD}|=|\overrightarrow{TD}|\)
\(|\overrightarrow{AB}|+|\overrightarrow{CD}|=|\overrightarrow{TC}|+|\overrightarrow{CD}|\)
Mà theo bđt tam giác thì:
\(|\overrightarrow{TC}+\overrightarrow{CD}|\geq |\overrightarrow{TD}|\Rightarrow |\overrightarrow{AB}|+\overrightarrow{CD}|\geq |\overrightarrow{AB}+\overrightarrow{CD}|\)
Dấu "=" xảy ra khi \(T, C,D\) thẳng hàng và $C$ nằm giữa $T,D$
$\Leftrightarrow \overrightarrow{TC}, \overrightarrow{CD}$ cùng hướng
$\Leftrightarrow \overrightarrow{AB}, \overrightarrow{CD}$ cùng hướng
Vậy với $\overrightarrow{a}, \overrightarrow{b}$ bất kỳ thì $|\overrightarrow{a}|+|\overrightarrow{b}|\geq |\overrightarrow{a}+\overrightarrow{b}|$. Dấu "=" xảy ra khi $\overrightarrow{a}, \overrightarrow{b}$ cùng hướng.
------------------
Áp dụng vào bài toán:
\(|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|\leq |\overrightarrow{a}+\overrightarrow{b}|+|\overrightarrow{c}|\leq |\overrightarrow{a}|+|\overrightarrow{b}|+|\overrightarrow{c}|\)
Dấu "=" xảy ra khi \(\overrightarrow{a}, \overrightarrow{b}\) cùng hướng và \(\overrightarrow{a}+\overrightarrow{b}, \overrightarrow{c}\) cùng hướng
\(\Leftrightarrow \overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}\) cùng hướng
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
\(\)vectơ \(\overrightarrow c = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\overrightarrow b \) có độ dài gấp \(\frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}\) lần vectơ \(\overrightarrow b \) và cùng hướng với vectơ \(\overrightarrow b \)
+) Nếu hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng thì hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \)cùng hướng và ngược lại
+) \(\left| {\overrightarrow c } \right| = \left| {\frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\overrightarrow b } \right| = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\left| {\overrightarrow b } \right| = \left| {\overrightarrow a } \right|\). Suy ra hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \)có cùng độ dài
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a)
Cách 1:
Ta có: \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
\( \Leftrightarrow \overrightarrow {KA} = - 2\overrightarrow {KB} \)
Suy ra vecto \(\overrightarrow {KA} \) và vecto\(\;\overrightarrow {KB} \) cùng phương, ngược chiều và \(KA = 2.KB\)
\( \Rightarrow K,A,B\)thẳng hàng, K nằm giữa A và B thỏa mãn: \(KA = 2.KB\)
Cách 2:
Ta có: \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
\(\begin{array}{l} \Leftrightarrow \left( {\overrightarrow {KB} + \overrightarrow {BA} } \right) + 2\overrightarrow {KB} = \overrightarrow 0 \\ \Leftrightarrow 3.\overrightarrow {KB} + \overrightarrow {BA} = \overrightarrow 0 \\ \Leftrightarrow 3.\overrightarrow {KB} = \overrightarrow {AB} \\ \Leftrightarrow \overrightarrow {KB} = \frac{1}{3}\overrightarrow {AB} \end{array}\)
Vậy K thuộc đoạn AB sao cho \(KB = \frac{1}{3}AB\).
b)
Với O bất kì, ta có:
\(\frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB} = \frac{1}{3}\left( {\overrightarrow {OK} + \overrightarrow {KA} } \right) + \frac{2}{3}\left( {\overrightarrow {OK} + \overrightarrow {KB} } \right) = \left( {\frac{1}{3}\overrightarrow {OK} + \frac{2}{3}\overrightarrow {OK} } \right) + \left( {\frac{1}{3}\overrightarrow {KA} + \frac{2}{3}\overrightarrow {KB} } \right) = \overrightarrow {OK} + \frac{1}{3}\left( {\overrightarrow {KA} + 2\overrightarrow {KB} } \right) = \overrightarrow {OK}\)
Vì \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \)
Vậy với mọi điểm O, ta có \(\overrightarrow {OK} = \frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB} .\)
BT
12 tháng 5 2017
Do \(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}\) nên hai véc tơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) đối nhau.
a)
\(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}\) nên O là trung điểm của AB.
b) \(\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}\) nên \(O\equiv B\).
Cách 1:
Gọi tọa độ của vectơ \(\overrightarrow a \) là (x; y).
Ta có: \(|\overrightarrow a |\, = \sqrt {{x^2} + {y^2}} \).
Đặt \(\overrightarrow i = \frac{1}{{|\overrightarrow a |}}\;.\overrightarrow a \)
\( \Rightarrow \overrightarrow i = \frac{1}{{\sqrt {{x^2} + {y^2}} }}.(x;y) = \left( {\frac{x}{{\sqrt {{x^2} + {y^2}} }};\frac{y}{{\sqrt {{x^2} + {y^2}} }}} \right)\)
\( \Rightarrow |\overrightarrow i |\, = \sqrt {{{\left( {\frac{x}{{\sqrt {{x^2} + {y^2}} }}} \right)}^2} + {{\left( {\frac{y}{{\sqrt {{x^2} + {y^2}} }}} \right)}^2}} = \sqrt {\frac{{{x^2}}}{{{x^2} + {y^2}}} + \frac{{{y^2}}}{{{x^2} + {y^2}}}} = 1\)
Mặt khác:
\(\overrightarrow i = \frac{1}{{|\overrightarrow a |}}\;.\overrightarrow a = \frac{1}{{\sqrt {{x^2} + {y^2}} }}.\overrightarrow a \) và \(\frac{1}{{\sqrt {{x^2} + {y^2}} }} > 0\) với mọi \(x,y \ne 0\)
Do đó vectơ \(\overrightarrow i \) và \(\overrightarrow a \) cùng hướng.
Vậy \(\frac{1}{{|\overrightarrow a |}}\;\overrightarrow a \) (hay \(\frac{{\overrightarrow a }}{{|\overrightarrow a |}}\)) là một vectơ đơn vị, cùng hướng với vectơ \(\overrightarrow a \).
Cách 2:
Với mọi vectơ \(\overrightarrow a \ne \overrightarrow 0 \), ta có: \(|\overrightarrow a |\; > 0 \Rightarrow k = \frac{1}{{|\overrightarrow a |}} > 0\). Đặt \(\overrightarrow i = \frac{1}{{|\overrightarrow a |}}\;.\overrightarrow a = k.\overrightarrow a \)
\(\begin{array}{l} \Rightarrow |\overrightarrow i |\, = \;|k.\overrightarrow a |\; = \;|k|.|\overrightarrow a |\;\\ \Leftrightarrow \left| {\overrightarrow {\,i} \,} \right| = k.|\overrightarrow a |\; = \frac{1}{{|\overrightarrow a |}}.|\overrightarrow a | = 1\end{array}\)
Mặt khác: \(\overrightarrow i = \frac{1}{{|\overrightarrow a |}}\;.\overrightarrow a = k.\overrightarrow a \) và \(k > 0\)
Do đó vectơ \(\overrightarrow i \) và \(\overrightarrow a \) cùng hướng.
Vậy \(\frac{1}{{|\overrightarrow a |}}\;\overrightarrow a \) (hay \(\frac{{\overrightarrow a }}{{|\overrightarrow a |}}\)) là một vectơ đơn vị, cùng hướng với vectơ \(\overrightarrow a \).