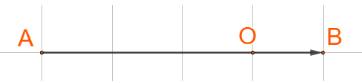
Cho hai điểm phân biệt A và B.
a) Hãy xác định điểm K sao cho \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
b) Chứng minh rằng với mọi điểm O, ta có \(\overrightarrow {OK} = \frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB} .\)

a)
Cách 1:
Ta có: \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
\( \Leftrightarrow \overrightarrow {KA} = - 2\overrightarrow {KB} \)
Suy ra vecto \(\overrightarrow {KA} \) và vecto\(\;\overrightarrow {KB} \) cùng phương, ngược chiều và \(KA = 2.KB\)
\( \Rightarrow K,A,B\)thẳng hàng, K nằm giữa A và B thỏa mãn: \(KA = 2.KB\)
Cách 2:
Ta có: \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
\(\begin{array}{l} \Leftrightarrow \left( {\overrightarrow {KB} + \overrightarrow {BA} } \right) + 2\overrightarrow {KB} = \overrightarrow 0 \\ \Leftrightarrow 3.\overrightarrow {KB} + \overrightarrow {BA} = \overrightarrow 0 \\ \Leftrightarrow 3.\overrightarrow {KB} = \overrightarrow {AB} \\ \Leftrightarrow \overrightarrow {KB} = \frac{1}{3}\overrightarrow {AB} \end{array}\)
Vậy K thuộc đoạn AB sao cho \(KB = \frac{1}{3}AB\).
b)
Với O bất kì, ta có:
\(\frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB} = \frac{1}{3}\left( {\overrightarrow {OK} + \overrightarrow {KA} } \right) + \frac{2}{3}\left( {\overrightarrow {OK} + \overrightarrow {KB} } \right) = \left( {\frac{1}{3}\overrightarrow {OK} + \frac{2}{3}\overrightarrow {OK} } \right) + \left( {\frac{1}{3}\overrightarrow {KA} + \frac{2}{3}\overrightarrow {KB} } \right) = \overrightarrow {OK} + \frac{1}{3}\left( {\overrightarrow {KA} + 2\overrightarrow {KB} } \right) = \overrightarrow {OK}\)
Vì \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \)
Vậy với mọi điểm O, ta có \(\overrightarrow {OK} = \frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB} .\)