Cho ba điểm D, E, G. Vecto \(\overrightarrow v = \overrightarrow {DE} + ( - \overrightarrow {DG} )\) bằng vecto nào sau đây?
A. \(\overrightarrow {EG} \)
B. \(\overrightarrow {GE} \)
C. \(\overrightarrow {GD} \)
D. \(\overrightarrow {ED} \)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Vận dụng tính chất giao hoán ta có: \[\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \]
Chọn C.
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Vì \(\overrightarrow a = \overrightarrow {AB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} \) nên tứ giác MNBA là hình bình hành.
Nói cách khác B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \) và điểm A.
Tương tự, C là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \) và điểm B.
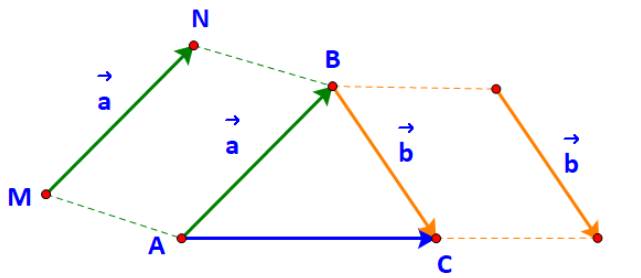
b) Dễ thấy: tổng của hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) là vecto \(\overrightarrow {AC} \).
Do đó tổng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)bằng vecto \(\overrightarrow {AC} \).
Ta có viết: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
28 tháng 11 2022
a: vecto DE
=vecto DA+vecto AE
=-2vecto AB+2/5*vecto AC
vecto DG=vecto DB+vecto BG
=-2*vecto AB-vecto GB
=-2vecto AB-(-vecto GA-vecto GC)
=-2 vecto AB-(vecto CG-vecto GA)
=-2vecto AB-(vecto CG+vecto AG)
=-2vecto AB+vecto GA+vecto GC
=-2*vecto AB+2*vecto GF
=-2vecto AB+2*1/3*vecto BF
=-2*vecto AB+2/3(vecto BA+vecto BC)
=-2vecto AB-2/3vecto AB+2/3*veto BC
=-8/3vecto AB+2/3*(vecto BA+vecto AC)
=-10/3vecto AB+2/3vecto AC
b: vecto DE=-2vecto AB+2/5vecto AC
vecto DG=-10/3vecto AB+2/3*vecto AC
Vì \(\dfrac{-2}{-\dfrac{10}{3}}=2:\dfrac{10}{3}=\dfrac{6}{10}=\dfrac{3}{5}=\dfrac{2}{5}:\dfrac{2}{3}\)
nên D,E,G thẳng hàng
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(2\overrightarrow{y}-\overrightarrow{z}=2\overrightarrow{a}-2\overrightarrow{b}-2\overrightarrow{c}+3\overrightarrow{b}+2\overrightarrow{c}=2\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{x}\)
\(\Rightarrow\) Ba vecto \(\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}\) đồng phẳng
13 tháng 8 2019
\(a\text{) }\overrightarrow{AB}-\overrightarrow{CD}=\left(\overrightarrow{AC}+\overrightarrow{CB}\right)-\overrightarrow{CD}\\ =\overrightarrow{AC}-\left(\overrightarrow{CD}-\overrightarrow{CB}\right)=\overrightarrow{AC}-\overrightarrow{BD}\)
\(b\text{) }\overrightarrow{AB}+\overrightarrow{DC}+\overrightarrow{BD}+\overrightarrow{CA}=\left(\overrightarrow{AB}+\overrightarrow{BD}\right)+\left(\overrightarrow{DC}+\overrightarrow{CA}\right)\\ =\left(\overrightarrow{AB}+\overrightarrow{BD}\right)+\left(\overrightarrow{DC}+\overrightarrow{CA}\right)=\overrightarrow{AD}+\overrightarrow{DA}=0\)
\(c\text{) }\overrightarrow{AC}+\overrightarrow{DE}-\overrightarrow{DC}-\overrightarrow{CE}+\overrightarrow{CB}\\ =\left(\overrightarrow{AC}+\overrightarrow{CB}\right)+\left(\overrightarrow{DE}-\overrightarrow{DC}\right)-\overrightarrow{CE}\\ =\overrightarrow{AB}+\overrightarrow{CE}-\overrightarrow{CE}=\overrightarrow{AB}\)
\(d\text{) }\overrightarrow{AB}+\overrightarrow{DE}+\overrightarrow{CF}\\ =\left(\overrightarrow{AC}+\overrightarrow{CB}\right)+\left(\overrightarrow{DF}+\overrightarrow{FE}\right)+\left(\overrightarrow{CE}+\overrightarrow{EF}\right)\\ =\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{CB}+\overrightarrow{DF}+\left(\overrightarrow{FE}+\overrightarrow{EF}\right)\\ =\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{CB}+\overrightarrow{DF}\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
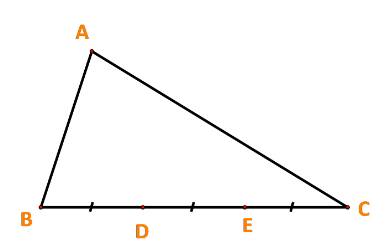
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \Leftrightarrow \overrightarrow {BC} = \overrightarrow b - \overrightarrow a \)
Lại có: vecto \(\overrightarrow {BD} ,\overrightarrow {BC} \) cùng hướng và \(\left| {\overrightarrow {BD} } \right| = \frac{1}{3}\left| {\overrightarrow {BC} } \right|\)
\( \Rightarrow \overrightarrow {BD} = \frac{1}{3}\overrightarrow {BC} = \frac{1}{3}(\overrightarrow b - \overrightarrow a )\)
Tương tự: vecto \(\overrightarrow {BE} ,\overrightarrow {BC} \) cùng hướng và \(\left| {\overrightarrow {BE} } \right| = \frac{2}{3}\left| {\overrightarrow {BC} } \right|\)
\( \Rightarrow \overrightarrow {BE} = \frac{2}{3}\overrightarrow {BC} = \frac{2}{3}(\overrightarrow b - \overrightarrow a )\)
Ta có:
\(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \Leftrightarrow \overrightarrow {AD} = \overrightarrow a + \frac{1}{3}(\overrightarrow b - \overrightarrow a ) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b \)
\(\overrightarrow {AB} + \overrightarrow {BE} = \overrightarrow {AE} \Leftrightarrow \overrightarrow {AE} = \overrightarrow a + \frac{2}{3}(\overrightarrow b - \overrightarrow a ) = \frac{1}{3}\overrightarrow a + \frac{2}{3}\overrightarrow b \)
Ta có: \(\overrightarrow {GD} = - \overrightarrow {DG} \)
\( \Rightarrow \overrightarrow v = \overrightarrow {DE} + ( - \overrightarrow {DG} ) = \overrightarrow {DE} + \overrightarrow {GD} \)
\( \Rightarrow \overrightarrow v = \overrightarrow {GD} + \overrightarrow {DE} = \overrightarrow {GE} \) (tính chất giao hóan)
Chọn B.