Cho ba điểm M, N, P. Vecto \(\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN} \) bằng vecto nào sau đây?
A. \(\overrightarrow {PN} \)
B. \(\overrightarrow {PM} \)
C. \(\overrightarrow {MP} \)
D. \(\overrightarrow {NM} \)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Ta có: \(\overrightarrow {GD} = - \overrightarrow {DG} \)
\( \Rightarrow \overrightarrow v = \overrightarrow {DE} + ( - \overrightarrow {DG} ) = \overrightarrow {DE} + \overrightarrow {GD} \)
\( \Rightarrow \overrightarrow v = \overrightarrow {GD} + \overrightarrow {DE} = \overrightarrow {GE} \) (tính chất giao hóan)
Chọn B.
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Vì \(\overrightarrow a = \overrightarrow {AB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} \) nên tứ giác MNBA là hình bình hành.
Nói cách khác B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \) và điểm A.
Tương tự, C là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \) và điểm B.
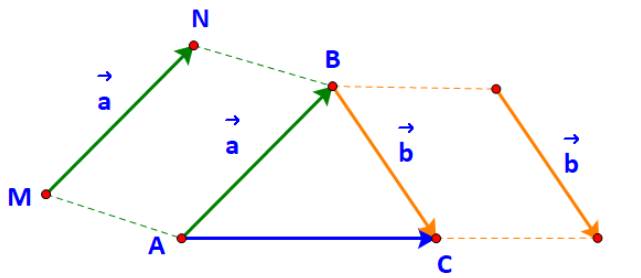
b) Dễ thấy: tổng của hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) là vecto \(\overrightarrow {AC} \).
Do đó tổng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)bằng vecto \(\overrightarrow {AC} \).
Ta có viết: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(2\overrightarrow{y}-\overrightarrow{z}=2\overrightarrow{a}-2\overrightarrow{b}-2\overrightarrow{c}+3\overrightarrow{b}+2\overrightarrow{c}=2\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{x}\)
\(\Rightarrow\) Ba vecto \(\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}\) đồng phẳng
B
6 tháng 9 2021
a)\(\overrightarrow{AB}+\overrightarrow{AN}=\overrightarrow{AM}\)
b)\(\overrightarrow{BA}+\overrightarrow{CN}=2\overrightarrow{BA}\)
c)Có \(\overrightarrow{AB}=\overrightarrow{NC}\)=>bt trở thành \(\overrightarrow{NC}+MC+\overrightarrow{MN}=\overrightarrow{MC}-\overrightarrow{MC}=vt0\)
d)có vt BA+vt BC=vtBN
bt trở thành vtMN-vtMN=vt0
hok tốt!
Vận dụng tính chất giao hoán ta có: \[\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \]
Chọn C.