Mũi tên xuất phát từ A đến B trong Hình 34 mô tả chuyển động (có hướng) của một máy bay trên đường băng.
Đoạn thẳng AB có hướng được gọi là gì?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 7 2021
- Gọi thời gian xuất phát là to, điểm gốc tại A, chiều dương là chiều từ A đến B .
- Theo bài ra ta có : \(\left\{{}\begin{matrix}x_1=30t\\x_2=L+40t\\x_{3.1}=L-50t\end{matrix}\right.\)
- Ta có : Khi xe 1 và xe 3 gặp nhau thì tổng quãng đường đi được là AB.
\(\Rightarrow80t=L\)
\(\Rightarrow t=\dfrac{L}{80}\)
=> Hai xe gặp nhau lại điểm cách A : \(\dfrac{30L}{80}=\dfrac{3L}{8}\left(km\right)\)
- Xét quá trình từ sau khi xe 1 gặp xe 3 :\(\left\{{}\begin{matrix}x_1=\dfrac{3L}{8}+30t^,\\x_2=40.\dfrac{L}{80}+L+40t^,\\x_3=\dfrac{3L}{8}+50t^,\end{matrix}\right.\)
- Để xe 2 đuổi kịp xe 3 thì \(\dfrac{3}{2}L+40t^,=\dfrac{3}{8}L+50t^,\)
Lại có : \(t=\dfrac{L}{80}\)
\(\Rightarrow t+t^,=0,09=\dfrac{L}{80}+t^,\)
- Giair hệ ta được : \(\left\{{}\begin{matrix}L=0,72\left(km\right)\\t^,=0,081\left(h\right)\\t=0,009\left(h\right)\end{matrix}\right.\)
b, Ta có : \(d_{3-1}=\dfrac{3}{8}L+50t^,-\dfrac{3}{8}L-30t^,=1,62\left(km\right)\)
Vậy ,....
2 tháng 7 2021
- Gọi chiều dương là chiều từ người đi bộ hướng tới người đi xe đạp , thời gian gốc là to, điểm mốc tại người đi bộ và khoảng cách giữa người đi bộ và đi xe đạp là x0 ( km, x > 0 ) và 3 người xe đạp, bộ, xe máy lần lượt là 1,2,3 .
- Theo bài ra ta có : \(\left\{{}\begin{matrix}x_1=x_0+20t\\x_2=vt\\x_3=-2x_0+60t\end{matrix}\right.\)
- Để 3 người cùng gặp nhau tại 1 điểm .
=> \(x_1=x_2=x_3=x\)
\(\Rightarrow x_0=\dfrac{40}{3}t\)
\(\Rightarrow x=\dfrac{100}{3}t=vt\)
\(\Rightarrow v=\dfrac{100}{3}\left(km/h\right)\)
Vậy ...
VT
29 tháng 5 2018
Phương trình chuyển động của xe máy xuất phát từ A chuyển động nhanh dần đều không vận tốc đầu với gia tốc a 1 = 2,5. 10 - 2 m/ s 2 :
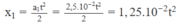
Phương trình chuyển động của xe máy xuất phát từ B cách A một đoạn x 0 = 400 m chuyển động nhanh dần đều không vận tốc đầu với gia tốc a 2 = 2,0. 10 - 2 m/ s 2 :
Đoạn thẳng AB có hướng được gọi là vecto \(\overrightarrow {AB} \).