RGBT:
(1+1/2)(1+1/4)(1+1/16)..........(1+1/22n)
Chú ý:bài này thuộc phần hiệu 2 bình phương.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 6 2023
a. Năm nguyên tử thuộc 2 nguyên tố hoá học.
b. Với p = 6:
- Nguyên tố đó là carbon/cacbon.
- KHHH: C
- NTK: 12 đvC (hoặc amu)
c. Với p = 20
- Nguyên tố đó là calcium/canxi
- KHHH: Ca
- NTK: 40 đvC (hoặc amu)
TP
4 tháng 8 2021
a) Năm nguyên tử này thuộc 2 nguyên tố hóa học
b) Z= 6 (Cacbon), kí hiệu là C
(1) (6p + 6n) => A=Z+N =6+6= 12
(3) (6p + 7n) => A=Z+N =6+7= 13
Z= 20 (Canxi), kí hiệu là Ca
(2) (20p + 20n) => A=Z+N =20+ 20= 40
(4) (20p + 22n) => A=Z+N =20+ 22= 42
(5) (20p + 23n) => A=Z+N =20+ 23= 43
c)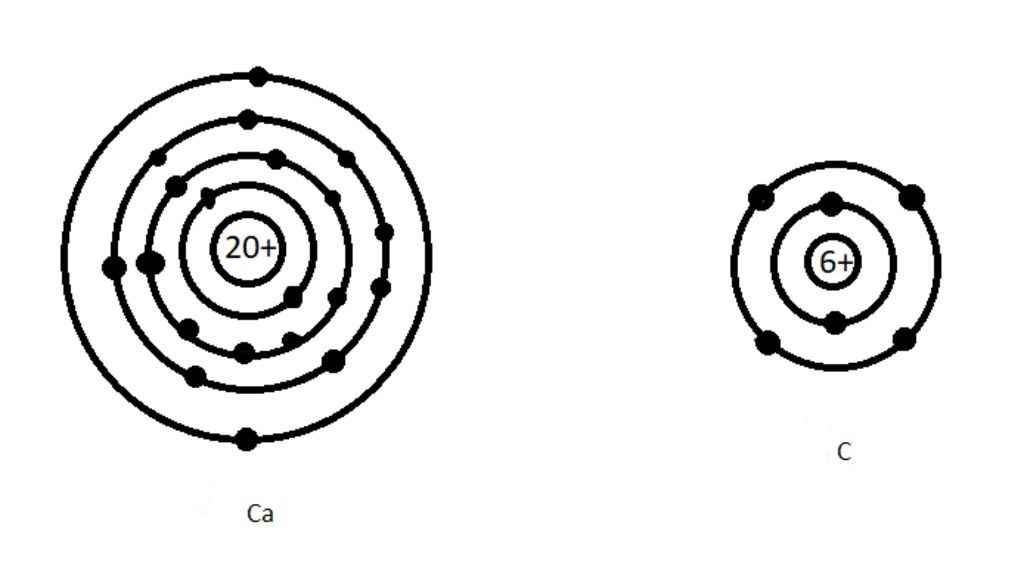
17 tháng 12 2017
Các nguyên tử này thuộc 2 nguyên tố hóa học.
Nguyên tử (1), (3) thuộc cùng 1 nguyên tố do cùng có 6p
Nguyên tử (2), (4), (5) thuộc cùng 1 nguyên tố do cùng có 20p.
21 tháng 8 2021
a) 5 nguyên tử này thuộc 2 nguyên tố hóa học:
b) - Nguyên tố Cacbon (C): Nguyên tử (1),nguyên tử (3)
NTK(C)=12 (đ.v.C)
NTK(1)= 6+6=12(đ.v.C); NTK(3)= 6+7=13(đ.v.C)
- Nguyên tố Canxi (Ca): Nguyên tử (2), nguyên tử (4) và nguyên tử (5)
NTK(Ca)=40(đ.v.C)
NTK(2)=20+20=40(đ.v.C); NTK(4)=20+22=42(đ.v.C); NTK(5)= 20+23=43(đ.v.C)
MN
20 tháng 6 2021
(1) Hạt nhân có : 6 proton , 6 notron.
(2) Hạt nhân có : 20 proton , 20 notron.
(3) Hạt nhân có : 6 proton , 7 notron.
(4) Hạt nhân có : 20 proton , 22 notron.
(5) Hạt nhân có : 20 proton , 23 notron.
24 tháng 7 2017
a, 1-2x+x^2 = x^2 - 2x.1 + 1^2= (x-1)^2
b, 4y+4+y^2 = y^2 + 2y.2+ 2^2 = (y+2)^2
c, 1/16+1/2x+x^2 = x^2 + 2.x.\(\frac{1}{4}\)+ (1/4)^2 = (x+1/4)^2
d, 36x^2+12xy+y^2 = (6x)^2 + 2.6x.y + y^2 = (6x+y)^2
24 tháng 7 2017
a) \(1-2x+x^2=\left(1-x\right)^2=\left(x-1\right)^2\)
b) \(4y+4+y^2=y^2+4y+4=\left(y+2\right)^2\)
c) \(\frac{1}{16}+\frac{1}{2}x+x^2=\left(x+\frac{1}{4}\right)^2\)
d) \(36x^2+12xy+y^2=\left(6x+y\right)^2\)
21 tháng 3 2023
2:
a: a^2-b^2
b: (a-b)^2
c: 1/2(a^2+b^2)
d: 1/2(a^3+b^3)
27 tháng 7 2017
Ta có:
\(\frac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}=\frac{1}{\sqrt{n\left(n+1\right)}\left(\sqrt{n+1}+\sqrt{n}\right)}\)
\(=\frac{\left(\sqrt{n+1}-\sqrt{n}\right)}{\sqrt{n\left(n+1\right)}}=\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\)
Thế vô bài toán được
\(\frac{1}{2\sqrt{1}+1\sqrt{2}}+\frac{1}{3\sqrt{2}+2\sqrt{3}}+...+\frac{1}{2016\sqrt{2015}+2015\sqrt{2016}}\)
\(=\frac{1}{\sqrt{1}}-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{2015}}-\frac{1}{\sqrt{2016}}\)
\(=1-\frac{1}{\sqrt{2016}}\)