Viết năm số chính phương đầu theo thứ tự tăng dần. Từ đó, dự đoán công thức tính số chính phương thứ n.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Năm số hạng đầu của dãy số: 1; 3; 5; 7; 9.
b) Công thức biểu diễn số hạng \({u_n}\) theo số hạng \({u_{n - 1}}\) là: \({u_n} = {u_{n - 1}} + 2\;\left( {n \ge 2} \right)\).
10 tháng 2 2023
4 số tự nhiên liên tiếp là n,n+1,n+2,n+3
viết theo hàng nghìn,trăm,chục ,đơn vị là
1000n+100(n+1)+10(n+2)+n+3=1111n+123
viết theo thứ tự ngược lại là
1000(n+3)+100(n+2)+10(n+1)+n=1111n+321...
vậy lớn hơn số ban đầu là 3210-123=3087
10 tháng 2 2023
Gọi số hàng nghìn là a \(\Rightarrow\) 0<a<10
Số cần tìm là:
a.\(10^3\) +(a-1).\(10^2\) + (a+1).10 + (a+2)
a.(\(10^3\) + \(10^2\)+10+1) - 100 + 10 + 2
1111.a - 88 = 11.101.a - 8.11
11(101.a-8)
=> 101.a-8=11.\(n^2\)
( 101a - 8) chia hết 11
101 chia 11 dư 2 và -8 chia 11 dư 3
=> a=4
Với a = 4 => \(\dfrac{101.4-8}{11}=36=6^2\)
Vậy số cần tìm là: 4356
CM
21 tháng 9 2019
a. Năm số hạng đầu của dãy số
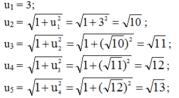
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
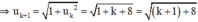
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Các số chính phương nhỏ hơn 50: \(1;4;9;16;25;36;49\).
b) Công thức số hạng tổng quát \({u_n} = {n^2},\;\left( {n\; \in {N^*}} \right)\).
20 tháng 4 2022
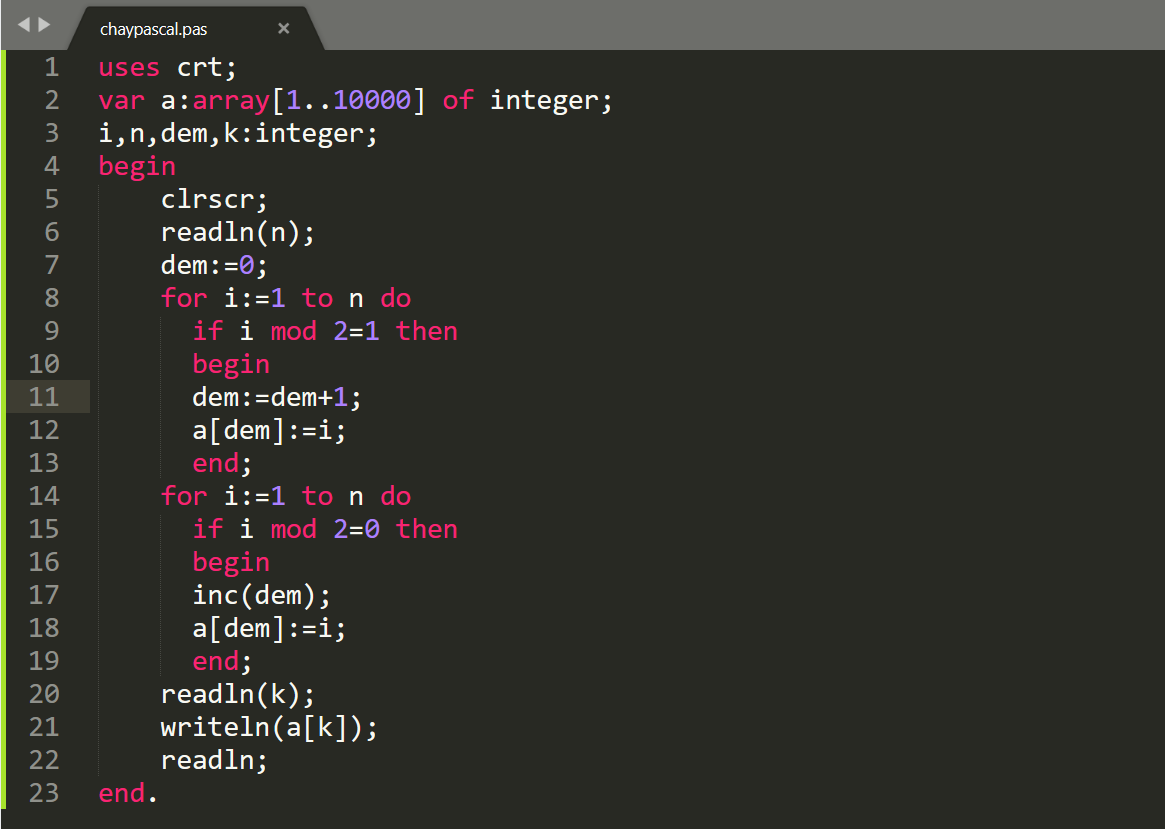
uses crt;
var a:array[1..100]of integer;
i,n,t,kt,j:integer;
begin
clrscr;
readln(n);
for i:=1 to n do readln(a[i]);
t:=0;
for i:=1 to n do
if a[i] mod 2<>0 then t:=t+a[i];
writeln(t);
for i:=1 to n do
if trunc(sqrt(a[i]))=sqrt(a[i]) then write(a[i]:4);
writeln;
for i:=1 to n do
if a[i]>1 then
begin
kt:=0;
for j:=2 to trunc(sqrt(a[i])) do
if a[i] mod j=0 then kt:=1;
if kt=0 then write(a[i]:4);
end;
readln;
end.
9 tháng 1 2017
để mình xem đáp án là số nào
gọi hàng nghìn là a => 0<a<10
so can tim có dang
a.10^3+(a-1).10^2+(a+1).10+(a+2)
a.(10^3+10^2+10+1)-100+10+2
1111.a-88=11.101.a-8.11=11(101.a-8)
=> 101.a-8=11n^2
\(\left(101.a-8\right)⋮11\)
101 chia 11 dư 2
-8 chia 11 dư 3
=> để chia hết cho 11 a chia 11 dư 4=> a=4 (duy nhất có thể chưa đủ)
với a=4 có \(\frac{101.4-8}{11}=36=6^2\)(Đủ =>nhận)
số cần tìm là: 11^2.6^2
BO
8 tháng 1 2017
Số chính phương có chữ số tận cùng bằng 0; 1; 4; 5; 6; 9
Vậy sô chinh phương cần tìm có thể là : 1234; 2345; 3456; 6789.
1234 \(⋮\)2 nhưng không chia hết cho 22 => không phai số chính phương
2345 \(⋮\)5 nhưng không chia hết cho 52 => không phai số chính phương
3456 \(⋮\)2 và chia hết cho 22 => số chính phương
6789 \(⋮\)3 nhưng không chia hết cho 32 => không phai số chính phương
Vậy số chính phương cần tìm là 3456
Ta có: 1, 4, 9, 16, 25.
Công thức tính số chính phương là \({n^2},\;\left( {n\; \in {N^*}} \right)\).