Xét sự tương đương của hai phương trình sau:
\(\frac{{x - 1}}{{x + 1}} = 0\) và \({x^2} - 1 = 0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hai phương trình \(x - 1 = 0\)và \(\frac{{{x^2} - 1}}{{x + 1}} = 0\) có tương đương vì:
\(\begin{array}{l}\frac{{{x^2} - 1}}{{x + 1}} = 0\\ \Leftrightarrow \frac{{\left( {x - 1} \right).\left( {x + 1} \right)}}{{x + 1}} = 0\\ \Leftrightarrow x - 1 = 0\end{array}\)

a) *) x² + 2 = 0
x² = -2 (vô lý)
Vậy S₁ = ∅ (1)
*) x(x² + 2) = 0
x = 0
Vậy S₂ = {0} (2)
Từ (1) và (2) ⇒ hai phương trình đã cho không tương đương
b) *) |x - 1| = 2
x - 1 = 2 hoặc x - 1 = -2
+) x - 1 = 2
x = 3
+) x - 1 = -2
x = -2 + 1
x = -1
Vậy S₃ = {-1; 3}
*) (x + 1)(x - 3) = 0
x + 1 = 0 hoặc x - 3 = 0
+) x + 1 = 0
x = -1 (3)
+) x - 3 = 0
x = 3
Vậy S₄ = {-1; 3} (4)
Từ (3) và (4) ⇒ hai phương trình đã cho tương đương

Ta có x + 1 = x ⇔ 0x = 1 (vô lí) ⇒ phương trình vô nghiệm;
x 2 + 1 = 0 ⇔ x 2 = - 1 (vô lí) ⇒ phương trình vô nghiệm
⇒ Hai phương trình x + 1 = x và x 2 + 1 = 0 tương đương vì có cùng tập nghiệm.

Ta có: (1) 2x – 1 = 2 ⇔ 2x = 3 ⇔ x = 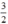
Phương trình 2x – 1 = 2 có tập nghiệm S = {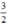 };
};
(2) (2x – 1)x = 2x ⇔ (2x – 1)x - 2x = 0 ⇔ x(2x - 1 – 2) = 0
⇔ x (2x - 3) = 0 ⇔ x = 0 hoặc 2x = 3 ⇔ x = 0 hoặc x = 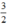
Phương trình (2x – 1)x = 2x có tập nghiệm S = { 0; 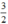 }
}
Vậy hai phương trình 2x – 1 = 2 và (2x – 1)x = 2x không tương đương vì không có cùng tập nghiệm

Câu 1:
A: Hai phương trình này tương đương vì có chung tập nghiệm S={-3}
B: Hai phương trình này không tương đương vì hai phương trình này không có chung tập nghiệm
Câu 2:
\(\left(y-2\right)^2=y+4\)
\(\Leftrightarrow y^2-4y+4-y-4=0\)
\(\Leftrightarrow y\left(y-5\right)=0\)
=>y=0 hoặc y=5

Ta có 3x = 3 ⇔ 3x – 3 = 0 ⇔ 3(x – 1) = 0 ⇔ 3(x – 1) : 3 = 0 : 3 ⇔ x – 1 = 0
Vậy 3x = 3 ⇔ x – 1 = 0

Phương trình x – 2 = 0 có tập nghiệm S = {2},
phương trình (x - 2)(x - 3) = 0 có tập nghiệm S = {2; 3}
Vậy 2 phương trình x - 2 = 0 và (x - 2)(x - 3) = 0 không tương đương

a) Ta có: \(x^2-2x-3=0\)
\(\Leftrightarrow x^2-3x+x-3=0\)
\(\Leftrightarrow x\left(x-3\right)+\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
Vậy: \(S_1=\left\{3;-1\right\}\)(1)
Ta có: \(\left(x+1\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-3\end{matrix}\right.\)
Vậy: \(S_2=\left\{-3;-1\right\}\)(2)
Từ (1) và (2) suy ra \(S_1\ne S_2\)
hay Hai phương trình \(x^2-2x-3=0\) và \(\left(x+1\right)\left(x+3\right)=0\) không tương đương với nhau
Ta có: \(\frac{{x - 1}}{{x + 1}}\;\)xác định khi \(x + 1 \ne 0 \Leftrightarrow x \ne - 1\)
\(\frac{{x - 1}}{{x + 1}} = 0 \Leftrightarrow x - 1 = 0 \Leftrightarrow x = 1\;\)
Tập nghiệm của phương trình là \({S_1} = \left\{ 1 \right\}\)
\({x^2} - 1 = 0 \Leftrightarrow {x^2} = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = - 1}\end{array}} \right.\;\)
Tập nghiệm của phương trình là \({S_2} = \left\{ {1; - 1} \right\}\)
Vậy tập nghiệm của 2 phương trình là không tương đương nhau