Quan sát đồ thị \(y = \cos x\) ở Hình 28
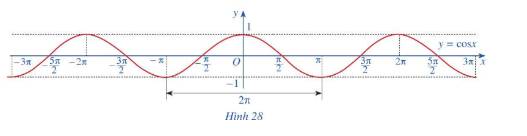
a) Nêu tập giá trị của hàm số \(y = \cos x\)
b) Trục tung có là trục đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \cos x\)
c) Bằng cách dịch chuyển đồ thị \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị có hàm số \(y = \cos x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\) hay không? Hàm số \(y = \cos x\) có tuần hoàn hay không?
d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \cos x\)

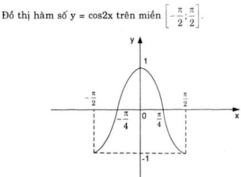
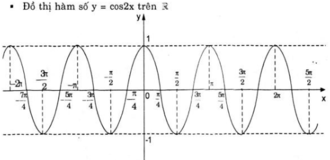
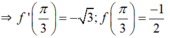
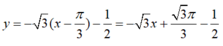
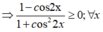
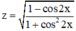 luôn xác định với mọi x ∈ R.
luôn xác định với mọi x ∈ R.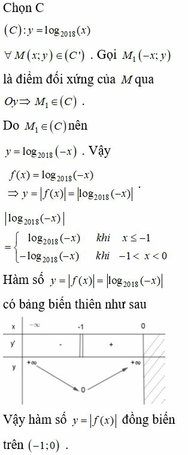
a) Tập giá trị của hàm số \(y = \cos x\)là \(\left[ { - 1;1} \right]\)
b) Trục tung là trục đối xứng của hàm số \(y = \cos x\).
Như vậy hàm số \(y = \cos x\)là hàm số chẵn.
c) Bằng cách dịch chuyển đồ thị \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị có hàm số \(y = \cos x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy hàm số \(y = \cos x\) là hàm số tuần hoàn
d) Hàm số \(y = \cos x\)đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\) với \(k \in Z\)