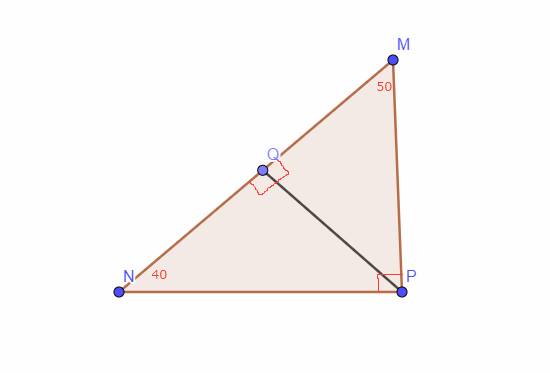
Cho tam giác MNP có đường cao PQ (Hình 17).

a) Viết công thức tính PQ theo cạnh n và góc a; công thức tính PQ theo cạnh m và góc b
b) Viết công thức tính diện tích mỗi tam giác MPQ, NPQ, MNP theo các cạnh m, n và các cạnh m, n và các góc a, b, a + b
c) Sử dụng kết quả: \({S_{MPN}} = {S_{MPQ}} + {S_{NPQ}}\), hãy tìm công thức tính \(\sin \left( {a + b} \right)\) theo \(\sin a,\cos a,\sin b,\cos b\). Từ đó rút ra đẳng \(\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b\,\,\,\left( * \right)\)
d) Tính \(\sin \left( {a - b} \right)\) bằng cách biến đổi \(\sin \left( {a - b} \right) = \sin \left[ {a + \left( { - b} \right)} \right]\) và sử dụng công thức (*)

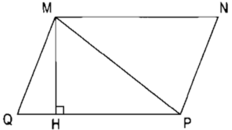
a) \(PQ = n.\cos a,PQ = m.\cos b\)
b) \(MQ = n.\sin a,PN = m.\sin b \Rightarrow MN = n.\sin a + m.\sin b\)
\(\begin{array}{l}{S_{MPQ}} = \frac{1}{2}m.\cos b.n.\sin a = \frac{1}{2}m.n.\cos b.\sin a\\{S_{NPQ}} = \frac{1}{2}n.\cos a.m.\sin b = \frac{1}{2}m.n.\cos a.\sin b\\{S_{MNP}} = \frac{1}{2}m.n.\sin \left( {a + b} \right)\end{array}\)
c) \({S_{MNP}} = {S_{MPQ}} + {S_{NPQ}} \Rightarrow \frac{1}{2}m.n.\cos b.\sin a + \frac{1}{2}m.n.\cos a.\sin b = \frac{1}{2}m.n.\sin \left( {a + b} \right)\)
\( \Rightarrow \sin \left( {a + b} \right) = \sin a.\cos b + \cos a.\sin b\)
d) \(\sin \left( {a - b} \right) = \sin \left[ {a + \left( { - b} \right)} \right] = \sin a.\cos \left( { - b} \right) + \cos a.\sin \left( { - b} \right) = \sin a.\cos b - \cos a.\sin b\)