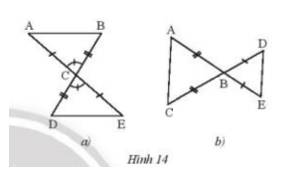
Hai tam giác trong mỗi hình bên (Hình 14a,b) có bằng nhau không? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Diện tích BAD = diện tích CAD (chung đáy AD, các đường cao vẽ từ B, C đến AD bằng nhau)
Diện tích ABC = diện tích BDC (chung đáy BC, các đường cao vẽ từ A và D đến BC bằng nhau)
Suy ra diện tích ABM bằng diện tích DCM
b, Diện tích ABC = diện tích DBC = diện tích OBC (chung đáy BC và 3 đường cao vẽ từ A, D, O đến BC bằng nhau)

a)Xét \(\Delta ABD\) và \(\Delta CDB\) có:
AB=CD (gt)
\(\widehat {ABD} = \widehat {CDB}\) (gt)
BD chung
Vậy \(\Delta ABD = \Delta CDB\)(c.g.c)
b)Xét \(\Delta OAD\) và \(\Delta OCB\) có:
AO=CO (gt)
\(\widehat {AOD} = \widehat {COB}\) (đối đỉnh)
OD=OB (gt)
Vậy \(\Delta OAD = \Delta OCB\)(c.g.c)

a) Vì \(K\)là giao điểm của \(AF\) và \(DC\) nên \(K \in CD\).
Vì \(ABCD\) là hình thang nên \(AB//CD \Rightarrow AB//CK\).
Xét tam giác \(ABF\) có \(CK//AB\) ta có:
\(\frac{{FA}}{{FK}} = \frac{{FB}}{{FC}}\) (hệ quả của định lí Thales)
Mà \(F\) lần lượt là trung điểm \(BC\) nên \(\frac{{FB}}{{FC}} = 1 \Rightarrow \frac{{FA}}{{FK}} = 1 \Rightarrow FA = FK\)
Xét tam giác \(ABF\) và tam giác \(KCF\) có:
\(FB = FC\) (chứng minh trên)
\(FK = FA\) (chứng minh trên)
\(\widehat {{F_1}} = \widehat {{F_2}}\)
Do đó, tam giác \(ABF\) bằng tam giác \(KCF\) (c – g – c).
b) Vì \(E\) là trung điểm của \(AD\);\(F\) là trung điểm của \(BC\) nên \(EF\) là đường trung bình của tam giác \(ADK\).
Do đó, \(EF//DK\) (tính chất)\( \Rightarrow EF//DC\)
Mà \(AB//CD \Rightarrow EF//AB//CD\) (điều phải chứng minh).
c) Vì \(EF\) là đường trung bình của tam giác \(ADK\) nên \(EF = \frac{1}{2}DK\).
Tam giác \(ABF\) bằng tam giác \(KCF\) nên \(AB = CK\) (hai cạnh tương ứng)
Ta có: \(DK = DC + CK \Rightarrow DK = DC + AB\).
Do đó, \[EF = \frac{1}{2}DK = \frac{1}{2}\left( {DC + AB} \right) = \frac{{DC + AB}}{2}\] (điều phải chứng minh).

Ta ghép như sau:
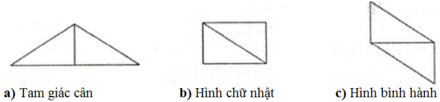
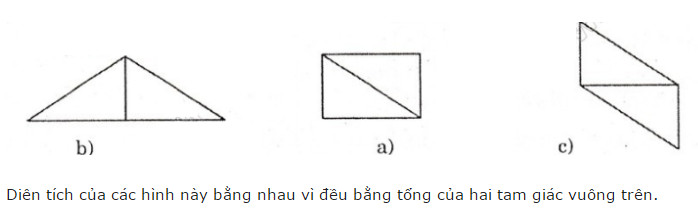
Diện tích 3 hình này đều bằng nhau vì cùng bằng tổng diện tích của hai tam giác vuông ban đầu.

ΔABC và ΔADC có
AC chung
Góc ACB = góc DCB
BC = DC
⇒ ΔABC = ΔADC ( cạnh – góc – cạnh)

a) Các mặt bên của mỗi hình a, b là các hình chữ nhật
Các mặt bên của mỗi hình c, d là hình tam giác
b) Hình c có cách cạnh bên bằng nhau và đáy là tam giác đều
c) Hình d có các cạnh bên bằng nhau và đáy là hình vuông
a:
1a,1b: Hình chữ nhật
1c,1d: Hình tam giác
b:
Cả bốn hình đều có các cạnh bên bằng nhau
1c,1a là hai hình là các đáy là tam giác đều
c: Hình 1b và hình 1d có đáy là hình vuông

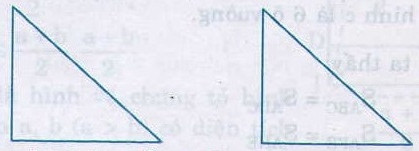
Cắt hai tam giác vuông bằng nhau từ một tấm bìa, chẳng hạn ta được hai hình sau:
Ghép hai tam giác trên để tạo thành:
a) Xét \(\Delta{ABC}\) và \(\Delta{EDC}\), ta có:
AC = CE
\(\widehat {ACB}\)= \(\widehat {DCE}\) ( 2 góc đối đỉnh )
CB = CD
\(\Rightarrow \Delta{ABC}=\Delta{EDC}\) (c.g.c)
b) Ta thấy 2 tam giác ABC và BDE không bằng nhau vì
\(AC \ne BE;BC \ne BD;DE \ne AC\)
* Hình 14a:
Xét ∆ABC và ∆EDC có:
BC = DC (giả thiết);
^ACB = ^ECD (hai góc đối đỉnh);
AC = EC (giả thiết).
Do đó ∆ABC = ∆EDC (c.g.c).
* Hình 14b:
Không có cạnh nào của tam giác ABC bằng với cạnh của tam giác EBD nên hai tam giác này không bằng nhau.
Vậy Hình 14a có ∆ABC = ∆EDC (c.g.c); Hình 14b hai tam giác ABC và EBC không bằng nhau.