Tìm số đo các góc chưa biết của các tam giác trong Hình 3 và cho biết tam giác nào là tam giác nhọn, tam giác nào là tam giác tù, tam giác nào là tam giác vuông.

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Hình tam giác có ba góc nhọn là tam giác ABC
- Hình tam giác có góc vuông là tam giác DEG
- Hình tam giác có góc tù là tam giác MNP

- Hình tam giác có ba góc nhọn là tam giác ABC
- Hình tam giác có góc vuông là tam giác DEG
- Hình tam giác có góc tù là tam giác MNP

- Hình tam giác MNP có ba góc nhọn .
- Hình tam giác ABC có góc vuông .
- Hình tam giác DEG có góc tù .

+) Ta có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow {50^o} + \widehat B + {40^o} = {180^o}\\ \Rightarrow \widehat B = {90^o}\end{array}\)
Vậy tam giác ABC là tam giác vuông.
+)
\(\begin{array}{l}\widehat D + \widehat E + \widehat F = {180^o}\\ \Rightarrow \widehat D + {55^o} + {63^o} = {180^o}\\ \Rightarrow \widehat D = {62^o}\end{array}\)
Vậy tam giác DEF là tam giác nhọn.
+)
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow {50^o} + \widehat N + {30^o} = {180^o}\\ \Rightarrow \widehat N = {100^o}\end{array}\)
Vậy tam giác MNP là tam giác tù.

Xét tam giác ABC có
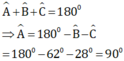
Vậy tam giác ABC là tam giác vuông.
Xét tam giác DEF có:
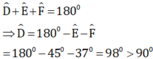
Vậy tam giác DEF là tam giác tù.
Xét tam giác HIK:
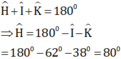
Nhận thấy
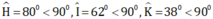
Vậy tam giác HIK là tam giác nhọn.
a) Vì tổng 3 góc trong tam giác là \({180^o}\)
Nên ta có :
\(\begin{array}{l} \Rightarrow \widehat {DEC} + \widehat {DCE} + \widehat {CDE} = {180^o}\\ \Rightarrow \widehat {DCE} = {180^o} - \widehat {DEC} - \widehat {CDE}\\ \Rightarrow \widehat {DCE} = {180^o} - {58^o} - {32^o} = {90^o}\end{array}\)
b) Theo đề bài ta có :
\(\begin{array}{l} \Rightarrow \widehat {HGF} + \widehat {GHF} + \widehat {GFH} = {180^o}\\ \Rightarrow \widehat {GFH} = {180^o} - \widehat {HGF} - \widehat {GHF}\\ \Rightarrow \widehat {GFH} = {180^o} - {68^o} - {42^o} = {70^o}\end{array}\)
c) Theo đề bài ta có :
\(\begin{array}{l} \Rightarrow \widehat {IJK} + \widehat {JKI} + \widehat {JIK} = {180^o}\\ \Rightarrow \widehat {JIK} = {180^o} - \widehat {IJK} - \widehat {JKI}\\ \Rightarrow \widehat {JIK} = {180^o} - {27^o} - {56^o} = {97^o}\end{array}\)