Cho hình chóp SABCD có đáy ABCD là hình bình hành.
a) Xác định giao tuyến của (SAB) và (SCD); (SAD) và (SBC).
b) Gọi M\(\in SC\), tìm giao tuyến của (ABM) và (SCD).
c) Gọi N\(\in SB\), tìm giao tuyến của (SAB) và (NCD).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

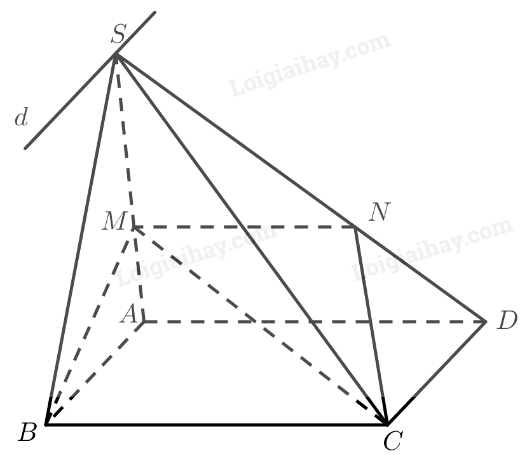
a) Ta có:
\(\left. \begin{array}{l}S \in \left( {SC{\rm{D}}} \right) \cap \left( {SAB} \right)\\C{\rm{D}}\parallel AB\\C{\rm{D}} \subset \left( {SC{\rm{D}}} \right)\\AB \subset \left( {SAB} \right)\end{array} \right\}\)
\( \Rightarrow \)Giao tuyến của hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {SAB} \right)\) là đường thẳng \(d\) đi qua \(S\), song song với \(C{\rm{D}}\) và \(AB\).
b) Ta có:
\(\begin{array}{l}BC = \left( {BCM} \right) \cap \left( {ABC{\rm{D}}} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\MN = \left( {BCM} \right) \cap \left( {SA{\rm{D}}} \right)\\BC\parallel A{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(A{\rm{D}}\parallel BC\parallel MN\).
Vậy tứ giác \(CBMN\) là hình thang.

- Ta có: AB thuộc (SAB)
CD thuộc (SCD)
Mà AB // CD, S là điểm chung của hai mặt phẳng (SAB) và (SCD).
Từ S kẻ Sx sao cho Sx // AB // CD.
Vậy Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).
- Tương tự ta có: Sy là giao tuyến của hai mặt phẳng (SAD) và (SBC) sao cho Sy // AD // BC.

Tham khảo:

a) Gọi E là giao điểm của AB và CD
Vì AB thuộc mp (SAB) nên E là giao điểm của CD và (SAB)
b) Ta có: S thuộc hai mặt phẳng (SAB) và (SCD)
E thuộc hai mặt phẳng (SAB) và (SCD)
Suy ra SE là giao tuyến của hai mặt phẳng (SAB) và (SCD)
c) Trong mp (SAB), gọi G là giao điểm của ME và SB
Mà SB thuộc (SBC), ME thuộc (MCD)
Do đó: G thuộc hai mặt phẳng (MCD) và (SBC)
C thuộc hai mặt phẳng (MCD) và (SBC)
Suy ra CG là giao tuyến của hai mặt phẳng (MCD) và (SBC).

2:
a: AD và BC là hai đường thẳng song song
b: \(S\in\left(SAB\right)\)
\(S\in\left(SCD\right)\)
Do đó:S là giao điểm của hai mặt phẳng (SAB) và (SCD)
c: AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó; \(\left(SAB\right)\cap\left(SCD\right)=mn\), mn đi qua S và mn//AB//CD

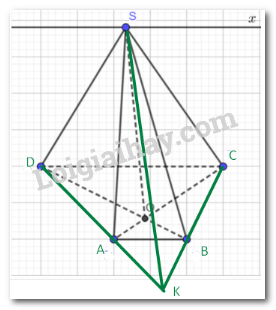
a) Gọi giao điểm của AD và BC là K.
Ta có: SK cùng thuộc mp(SAD) và (SBC).
Vậy SK là giao tuyến của (SAD) và (DBC).
b) (SAB) và (SCD) có AB // CD và S chung nên giao tuyến là dường thẳng Sx đi qua x và song song với AB và CD.
c) Gọi O là giao điểm của AC và BD suy ra O thuộc giao tuyến của (SAC) và (SBC)
Suy ra SO là giao tuyến của (SAC) và (SBD).

1: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
=>\(\left(SAC\right)\cap\left(SBD\right)=SO\)
AB//CD
S thuộc (SAB) giao (SCD)
=>(SAB) giao (SCD)=xy, xy qua S, xy//AB//DC
2:
Xét ΔSBC có SM/SB=SN/SC
nên MN//BC
=>MN//AD
=>AMND là hình thang
Xét ΔSBD có BM/BS=BO/BD
nên MO//SD
=>MO//(SAD)
a: Xét (SAB) và (SCD) có
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=mn, mn đi qua S và mn//AD//BC
c: \(N\in SB\subset\left(SAB\right);N\in\left(NCD\right)\)
=>\(N\in\left(SAB\right)\cap\left(NCD\right)\)
Xét (SAB) và (NCD) có
\(N\in\left(SAB\right)\cap\left(NCD\right)\)
AB//CD
Do đó: (SAB) giao (NCD)=ab, ab đi qua N và ab//CD//AB