Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Vì S và t là hai đại lượng tỉ lệ thuận nên \( \dfrac{1}{{ - 3}} = \dfrac{2}{?} = \dfrac{3}{?} = \dfrac{4}{?} = \dfrac{5}{?}\) ( tính chất đại lượng tỉ lệ thuận)
\(\Rightarrow t= - 3S\)
Thay S = 2 ta có : t= -3.2 = -6
Thay S = 3 ta có : t= -3.3 = -9
Thay S = 4 ta có : t= -3.4 = -12
Thay S = 5 ta có : t= -3.5 = -15
b) Từ câu a ta có công thức tính t theo S là : \(t = - 3S\)
a)
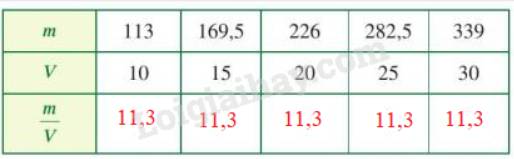
b) Hai đại lượng m và V tỉ lệ thuận với nhau vì tỉ lệ \(\dfrac{m}{V}\) không đổi.
c) Hệ số tỉ lệ của m đối với V là: 11,3
Công thức liên hệ: m = 11,3 . V
Vì m và n là hai đại lượng tỉ lệ nên \( \dfrac{2}{{ - 6}} = \dfrac{3}{{ - 9}} = \dfrac{4}{a} = \dfrac{b}{{ - 18}}\)
Ta được: \(\dfrac{2}{{ - 6}} = \dfrac{3}{{ - 9}} = \dfrac{4}{a} = \dfrac{b}{{ - 18}} = - \dfrac{1}{3}\)
\( \Rightarrow \dfrac{4}{a} = - \dfrac{1}{3}\) và \(\dfrac{b}{{ - 18}} = - \dfrac{1}{3}\)
\( \Rightarrow a = - 3.4 = - 12\) và \(3b = 18 \Rightarrow b = 6\)
a) Đại lượng x tỉ lệ thuận với đại lượng f do f và x liên hệ với nhau theo công thức f = 5x .
\( \Rightarrow x = \dfrac{1}{5}y\)
\( \Rightarrow \) Hệ số tỉ lệ là : \(\dfrac{1}{5}\)
b) Theo đề bài ta có P tỉ lệ thuận với đại lượng m theo hệ số tỉ lệ g = 9,8 nên ta có công thức :
P = 9,8m ( hệ số k = g = 9,8 )
Ta có : \(\dfrac{n}{m} = \dfrac{{ - 2}}{?} = \dfrac{{ - 1}}{?} = \dfrac{0}{?} = \dfrac{1}{{ - 5}} = \dfrac{2}{?}\) \( \Rightarrow \dfrac{n}{m} = \dfrac{1}{{ - 5}}\) \( \Rightarrow m = - 5n\)
Thay \(n = - 2 \Rightarrow m = ( - 2).( - 5) = 10\) \( \Rightarrow ? = 10\)
Thay \(n = - 1 \Rightarrow m = ( - 1).( - 5) \Rightarrow ? = 5\)
Thay \(n = 0 \Rightarrow m = 0.( - 5) \Rightarrow ? = 0\) nhưng ? là mẫu số nên \(? \ne 0\) \( \Rightarrow ? \in \emptyset \)
Thay \(n = 2 \Rightarrow m = 2.( - 5) \Rightarrow ? = - 10\)