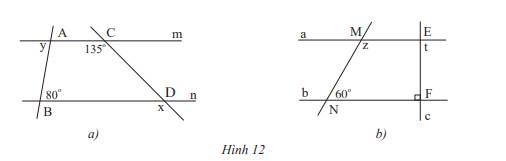
Cho biết m // n và a // b. Tính số đo x,y,z và t của các góc trong hình 12.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
Đối đỉnh: góc tMx và góc yMz; góc tMy và góc xMz
Kề bù: góc tMz và góc tMy; góc yMz và góc xMz
b: Kề bù: góc MNA và góc MNx; góc MAN và góc zAM
c: Đối đỉnh: góc AIB và góc MIN; góc AIM và góc BIN
Kề bù: góc AIB và góc AIM
góc MIN và góc BIN

Ta có: a ⊥ P Q ; b ⊥ P Q (gt).
Þ a // b (vì cùng vuông góc với PQ).
Do đó: x + 75 ° = 180 ° (cặp góc trong cùng phía)
x = 180 ° − 75 ° = 105 ° .

a) Ta có: \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\end{array} \right.\).
b) Xét tam giác \(DEF\) có:
\(\widehat D + \widehat E + \widehat F = 180^\circ \) (tổng ba góc trong một tam giác).
Ta có: \(\widehat D = 78^\circ ;\widehat E = 57^\circ \) thay số ta được
\(78^\circ + 57^\circ + \widehat F = 180^\circ \Rightarrow \widehat F = 180^\circ - 78^\circ - 57^\circ = 45^\circ \)
Ta có: \(\Delta DEF\backsim\Delta D'E'F' \Rightarrow \widehat D = \widehat {D'};\widehat E = \widehat {E'};\widehat F = \widehat {F'}\) (các góc tương ứng bằng nhau)
Do đó, \(\widehat D = \widehat {D'} = 78^\circ ;\widehat F = \widehat {F'} = 45^\circ \).
c) Ta có \(\Delta MNP\backsim\Delta M'N'P' \Rightarrow \frac{{MN}}{{M'N'}} = \frac{{MP}}{{M'P'}} = \frac{{NP}}{{N'P'}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Với \(MP = 10;NP = 6;M'N' = 15;N'P' = 12\) thay vào ta được:
\( \Rightarrow \left\{ \begin{array}{l}\frac{{MN}}{{15}} = \frac{1}{2}\\\frac{{10}}{{M'P'}} = \frac{1}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}MN = \frac{{15.1}}{2} = 7,5\\M'P' = \frac{{10.2}}{1} = 20\end{array} \right.\).
Vậy \(MN = 7,5;M'P' = 20\).
a) Vì m // n nên x = 135\(^\circ \)( 2 góc đồng vị) ; y = 80\(^\circ \) ( 2 góc so le trong)
b)
Vì a // b nên \(\widehat {{M_1}} = 60^\circ \) ( 2 góc đồng vị)
Mà \(\widehat {{M_1}} + z = 180^\circ \) ( 2 góc kề bù) nên z = 180\(^\circ \)- 60\(^\circ \)=120\(^\circ \)
Vì a // b nên \(\widehat {{F_1}} = t\) ( 2 góc so le trong), mà \(\widehat {{F_1}} = 90^\circ \) nên t = 90\(^\circ \)