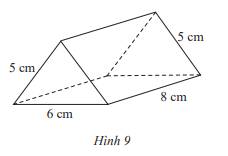
Tạo lập hình lăng trụ đứng tam giác với kích thước như Hình 9.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}BB' \bot \left( {A'B'C'} \right) \Rightarrow BB' \bot A'B'\\A'B' \bot B'C'\end{array} \right\} \Rightarrow A'B' \bot \left( {CC'B'B} \right)\\ \Rightarrow \left( {CA',\left( {CC'B'B} \right)} \right) = \left( {CA',CB'} \right) = \widehat {A'CB'}\\B'C = \sqrt {BB{'^2} + B{C^2}} = 2\sqrt {61} ,A'B' = AB = 4\\\tan \widehat {A'CB'} = \frac{{A'B'}}{{B'C}} = \frac{2}{{\sqrt {61} }} \Rightarrow \widehat {A'CB'} \approx 14,{4^ \circ }\end{array}\)
Vậy \(\left( {CA',\left( {CC'B'B} \right)} \right) \approx 14,{4^ \circ }\)
b) \(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot AC,CC' \bot BC\)
Vậy \(\widehat {ACB}\) là góc nhị diện cạnh \(CC'\).
\(\tan \widehat {ACB} = \frac{{AB}}{{AC}} = \frac{1}{3} \Rightarrow \widehat {ACB} \approx 18,{4^ \circ }\)
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Diện tích đáy của lăng trụ là:
\(\dfrac{1}{2}.3.6+\dfrac{1}{2}.4.6\) = 21 (cm2)
Tính thể tích lăng trụ đứng là:
V = Sđáy . h = 21.7 = 147 (cm3)
2 tháng 8 2023
Ta có Sxq= chu vi đáy (hình bình hành) nhân chiều cao= 2.(7+13).2=80 cm vuông
Ta có V(thể tích)= S đáy . Chiều cao=6.13.2=156 cm khối
Chúc bạn học tốt và nhớ đọc kỹ kiến thức trong sách giáo khoa
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Diện tích xung quanh của chiếc hộp là:
Sxq = Cđáy . h = (20+12+16). 25 = 1200 (cm2)
CM
27 tháng 12 2019
Chia hình ABCDE thành hai hình thang vuông có cạnh đáy nhỏ là 5m đáy lớn 8m, chiều cao là 4m.
Ta có: S A B C D E = 2.(5+8)/2 .4 = 52( m 2 )
Bước 1: Vẽ 3 hình chữ nhật với kích thước như sau:
Bước 2: Gấp các cạnh BN và CP sao cho cạnh AM trùng với A’M’, ta được hình lăng trụ đứng tam giác ABC.MNP cần tạo lập
Diện tích đáy hình lăng trụ là ::
\(\text{70 . 90 = 6300 ( cm ^2 )}\)
Thể tích hình lăng trụ là ::
\(\text{6300 . 60 = 378000 ( cm^3 )}\)
Công thức :V=S.h